题目内容
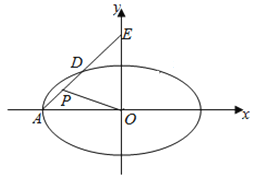
【题目】已知椭圆C：
过点A
，两个焦点为（-1，0），（1，0）。
（Ⅰ）求椭圆C的方程；
（Ⅱ）E,F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。
【答案】(1)
（2）直线
的斜率为定值
【解析】
试题(1) 由题意
，设椭圆方程为
，将
代入即可求出
，则椭圆方程可求.
(2)设直线AE方程为：
，代入入得
，再由点在椭圆上，根据结直线的斜率与
的斜率互为相反数，结合直线的位置关系进行求解．
（1）由题意，设椭圆方程为，
因为点在椭圆上，所以
，解得，
所求椭圆方程为
（2）设直线方程为，代入得
设
，
，点在直线上
则
，
；
直线的斜率与直线的斜率互为相反数，在上式中用
代替
得
，
，
直线的斜率
所以直线的斜率为定值
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
