题目内容
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,
,![]() ,第二组
,第二组![]() ,
,![]() ,
,![]() 第八组
第八组![]() ,
,![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.

【答案】(1)![]() ,绘图见解析;(2)
,绘图见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由频率分布直方图可得:各小矩形的高之和为0.1,运算可得解;
(2)由频率分布直方图中平均数的求法即可得解;
(3)样本成绩属于第六组的有![]() 人,样本成绩属于第八组的有
人,样本成绩属于第八组的有![]() 人,则随机抽取2名,
人,则随机抽取2名,
基本事件总数为![]() ,他们的分差的绝对值小于10分包含的基本事件个数为
,他们的分差的绝对值小于10分包含的基本事件个数为![]() ,再利用古典概型概率公式运算即可.
,再利用古典概型概率公式运算即可.
解:(1)由频率分布直方图得第七组的频率为:
![]() .
.
完成频率分布直方图如下:
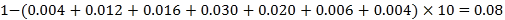
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分为:
![]()
![]() .
.
(3)样本成绩属于第六组的有![]() 人,样本成绩属于第八组的有
人,样本成绩属于第八组的有![]() 人,
人,
从样本成绩属于第六组和第八组的所有学生中随机抽取2名,
基本事件总数![]() ,
,
他们的分差的绝对值小于10分包含的基本事件个数![]() ,
,
故他们的分差的绝对值小于10分的概率![]() .
.

练习册系列答案
相关题目