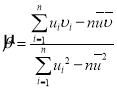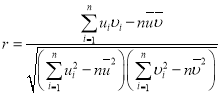题目内容
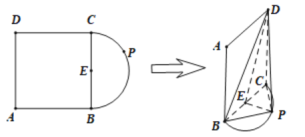
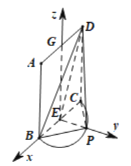
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)证明:![]() 平面
平面![]() .
.
(2)三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)利用面面垂直的性质定理证得![]() 平面
平面![]() ,由此证得
,由此证得![]() ,根据圆的几何性质证得
,根据圆的几何性质证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(2)判断出三棱锥![]() 的体积最大时
的体积最大时![]() 点的位置.建立空间直角坐标系,通过平面
点的位置.建立空间直角坐标系,通过平面![]() 和平面
和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值.
的余弦值.
(1)证明:因为平面![]() 平面
平面![]() 是正方形,
是正方形,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为点![]() 在以
在以![]() 为直径的半圆弧上,所以
为直径的半圆弧上,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:显然,当点![]() 位于
位于![]() 的中点时,
的中点时,![]() 的面积最大,三棱锥
的面积最大,三棱锥![]() 的体积也最大.
的体积也最大.
不妨设![]() ,记
,记![]() 中点为
中点为![]() ,
,
以![]() 为原点,分别以
为原点,分别以![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向,
轴的正方向,
建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则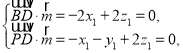 令
令![]() ,得
,得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则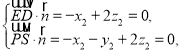 令
令![]() ,得
,得![]() ,
,
所以![]() .
.
由图可知,二面角![]() 为锐角,故二面角
为锐角,故二面角![]() 的余弦值为
的余弦值为![]() .
.

 教材全解字词句篇系列答案
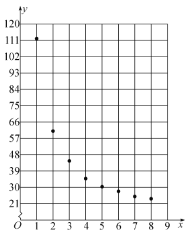
教材全解字词句篇系列答案【题目】自从新型冠状病毒爆发以来,全国范围内采取了积极的措施进行防控,并及时通报各项数据以便公众了解情况,做好防护.以下是湖南省2020年1月23日-31日这9天的新增确诊人数.
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
新增确诊人数 | 15 | 19 | 26 | 31 | 43 | 78 | 56 | 55 | 57 |
经过医学研究,发现新型冠状病毒极易传染,一个病毒的携带者在病情发作之前通常有长达14天的潜伏期,这个期间如果不采取防护措施,则感染者与一位健康者接触时间超过15秒,就有可能传染病毒.
(1)将1月23日作为第1天,连续9天的时间作为变量x,每天新增确诊人数作为变量y,通过回归分析,得到模型![]() 用于对疫情进行分析.对上表的数据作初步处理,得到下面的一些统计量的值(部分数据已作近似处理):
用于对疫情进行分析.对上表的数据作初步处理,得到下面的一些统计量的值(部分数据已作近似处理):![]() ,
,![]() .根据相关数据,求该模型的回归方程(结果精确到0.1),并依据该模型预测第10天新增确诊人数.
.根据相关数据,求该模型的回归方程(结果精确到0.1),并依据该模型预测第10天新增确诊人数.
(2)如果一位新型冠状病毒的感染者传染给他人的概率为0.3,在一次12人的家庭聚餐中,只有一位感染者参加了聚餐,记余下的人员中被感染的人数为![]() ,求
,求![]() 最有可能(即概率最大)的值是多少.
最有可能(即概率最大)的值是多少.
附:对于一组数据![]() ,
,![]() …,
…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为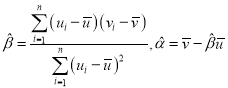 .
.
【题目】众所周知,大型网络游戏(下面简称网游)的运行必须依托于网络的基础上,否则会出现频繁掉线的情况,进而影响游戏的销售和推广,某网游经销在甲地区5个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线的测试,得到数据如下:
位置 类型 | A | B | C | D | E |
电信 | 4 | 3 | 8 | 6 | 12 |
网通 | 5 | 7 | 9 | 4 | 3 |
(1)如果在测试中掉线次数超过5次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过0.15的前提下,能否说明网络状况与网络的类型有关?
(2)若该游戏经销商要在上述接受测试的电信的5个地区中任选2个作为游戏推广,求A,B两地区至少选到一个的概率.
参考公式: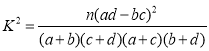 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|