题目内容
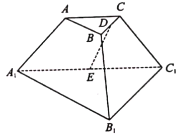
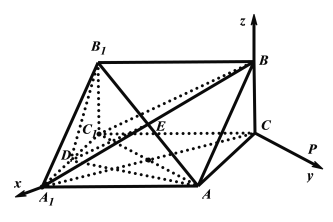
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的动点.
上的动点.
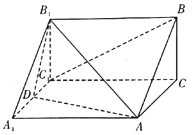
(1)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面ABC,且
平面ABC,且![]() 是否存在点
是否存在点![]() ,使二面角
,使二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连![]() 交
交![]() 与
与![]() ,连
,连![]() ,
,![]() 为
为![]() 中点,结合已知可得
中点,结合已知可得![]() ,即可证明结论;
,即可证明结论;
(2)根据已知可得![]() 平面
平面![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,由已知确定
为坐标原点建立空间直角坐标系,由已知确定![]() 坐标,假设满足条件的点
坐标,假设满足条件的点![]() 存在,设
存在,设![]() ,求出平面
,求出平面![]() 的法向量坐标,取平面
的法向量坐标,取平面![]() 一个法向量为
一个法向量为![]() ,按照空间向量的面面角公式,建立
,按照空间向量的面面角公式,建立![]() 的方程,求解即可得出结论.
的方程,求解即可得出结论.
(1)连![]() 交
交![]() 与
与![]() ,连
,连![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() 为
为![]() 中点,
中点,
又![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() 平行四边形
平行四边形![]() 为菱形,
为菱形,![]() ,
,
又平面![]() 平面ABC,平面
平面ABC,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
过点![]() 作
作![]() 的平行线
的平行线![]() ,即
,即![]() 两两互相垂直,
两两互相垂直,
以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线分别为
所在的直线分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() ,
,
故![]()
![]() ,
,
假设存在点![]() ,使二面角
,使二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,
,
设![]() ,
,
![]() ,
,
平面![]() 一个法向量为
一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
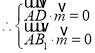 ,即
,即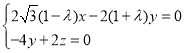 ,
,
令![]() ,则
,则![]() ,
,
![]()
由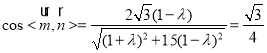 ,
,
整理得![]() 或
或![]() ,
,
解得![]() 舍去)或
舍去)或![]() ,
,
![]() ,
,
![]() 满足条件的点
满足条件的点![]() 存在,且
存在,且![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员![]() 人,其中
人,其中![]() 岁及以上的共有
岁及以上的共有![]() 人.这
人.这![]() 人中确诊的有
人中确诊的有![]() 名,其中
名,其中![]() 岁以下的人占
岁以下的人占![]() .
.
(1)请将下面的列联表补充完整,并判断是否有![]() %的把握认为是否确诊患新冠肺炎与年龄有关;
%的把握认为是否确诊患新冠肺炎与年龄有关;
确诊患新冠肺炎 | 未确诊患新冠肺炎 | 合计 | |
50岁及以上 | 40 | ||
50岁以下 | |||
合计 | 10 | 100 |
(2)为了研究新型冠状病毒的传染源和传播方式,从![]() 名确诊人员中随机抽出
名确诊人员中随机抽出![]() 人继续进行血清的研究,
人继续进行血清的研究,![]() 表示被抽取的
表示被抽取的![]() 人中
人中![]() 岁以下的人数,求
岁以下的人数,求![]() 的分布列以及数学期望.
的分布列以及数学期望.
参考表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式: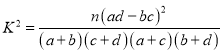 ,其中
,其中![]() .
.
【题目】众所周知,大型网络游戏(下面简称网游)的运行必须依托于网络的基础上,否则会出现频繁掉线的情况,进而影响游戏的销售和推广,某网游经销在甲地区5个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线的测试,得到数据如下:
位置 类型 | A | B | C | D | E |
电信 | 4 | 3 | 8 | 6 | 12 |
网通 | 5 | 7 | 9 | 4 | 3 |
(1)如果在测试中掉线次数超过5次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过0.15的前提下,能否说明网络状况与网络的类型有关?
(2)若该游戏经销商要在上述接受测试的电信的5个地区中任选2个作为游戏推广,求A,B两地区至少选到一个的概率.
参考公式: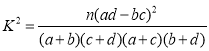 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|