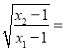题目内容
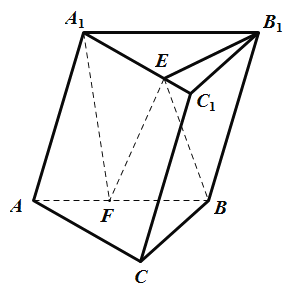
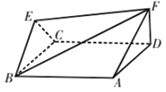
【题目】如图所示,菱形ABCD与正三角形BCE的边长均为2,它们所在的平面互相垂直,DF⊥平面ABCD且DF![]() .
.
(1)求证:EF//平面ABCD;
(2)若∠ABC=∠BCE,求二面角A﹣BF﹣E的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)要线面平行,即证直线在面外且直线平行于平面内的一条直线,故过点E作EH⊥BC于![]() 构造平行四边形即可得到线线平行.
构造平行四边形即可得到线线平行.
(2)连接HA,根据题意,AH⊥BC,以H为原点,HB,HA,HE为x,y,z轴建立空间直角坐标系,分别求出平面BAF和平面BEF的法向量,利用法向量求出二面角的余弦值.
(1)过点E作EH⊥BC,连接HD,EH![]() ,
,
因为平面ABCD⊥平面BCE,EH平面BCE,
平面ABCD∩平面BCE=BC,
所以EH⊥平面ABCD,
因为FD⊥ABCD,FD![]() ,
,
所以FD//EH,FD=EH,故平行四边形EHDF,
所以EF//HD,
由EF平面ABCD,HD平面ABCD,
所以EF//平面ABCD;
(2)连接HA,根据题意,AH⊥BC,
如图:
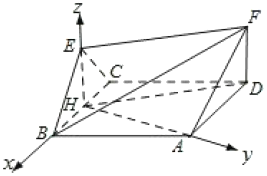
以H为原点,HB,HA,HE为x,y,z轴建立空间直角坐标系,
则A(0,![]() ,0),B(1,0,0),E(0,
,0),B(1,0,0),E(0,![]() ,
,![]() ),F(-2,
),F(-2,![]() ,
,![]() ),
),
则![]() (﹣1,
(﹣1,![]() ,0),
,0),![]() (﹣1,0,
(﹣1,0,![]() ),
),![]() (﹣3,
(﹣3,![]() ,
,![]() ),
),
设平面BAF的法向量为![]() (x,y,z),
(x,y,z),
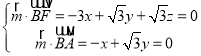 ,得
,得![]() (
(![]() ,1,2),
,1,2),
设平面BEF的法向量为![]() ,
,
由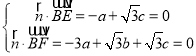 ,得
,得![]() ,
,
由cos![]() ,
,
所以二面角A﹣FB﹣E的余弦值为![]() .
.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目