题目内容
1.已知命题P:?b∈(-∞,2),f(x)=x2+bx+c在(-∞,-1)上为减函数;命题Q:?x0∈Z,使得2<1.则在命题¬P∨¬Q,¬P∧¬Q,P∨¬Q,P∧¬Q中任取一个命题,则取得真命题的概率是.分析 命题P:f(x)=+c-,?b∈(-∞,2),其对称轴为x=->-1,且开口向上,即可得出f(x)在(-∞,-1)上为减函数,即可判断出命题P的真假;对于命题Q:又由2<1,利用指数函数的性质可得解得x0<0,取x0=-1∈Z,满足条件,即可判断出命题Q真假,再利用复合命题真假的判定方法可得:在命题¬P∨¬Q,¬P∧¬Q,P∨¬Q,P∧¬Q中,只有P∨¬Q是真命题,再利用古典概率计算公式即可得出.
解答 解:命题P:?b∈(-∞,2),f(x)=x2+bx+c=+c-,其对称轴为x=->-1,
且开口向上,∴f(x)=x2+bx+c在(-∞,-1)上为减函数,∴命题P正确;
对于命题Q:又由2<1,解得x0<0,∴?x0=-1∈Z,满足条件,∴命题Q也正确.
在命题¬P∨¬Q,¬P∧¬Q,P∨¬Q,P∧¬Q中,只有P∨¬Q是真命题,其余都是假命题,
故由古典概型的概率计算公式可知取得真命题的概率是.
故答案为:.
点评 本题考查了复合命题真假的判定方法、古典概率计算公式,考查了推理能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如图所示:横轴为投资时间,纵轴为回报,根据以上信息,若使回报最多,下列说法错误的是( )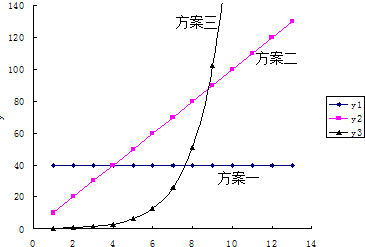

| A. | 投资3天以内(含3天),采用方案一 | B. | 投资4天,不采用方案三 | ||
| C. | 投资6天,采用方案二 | D. | 投资10天,采用方案二 |
16.已知O为坐标原点,双曲线=1(a,b>0)的右焦点F,以F为圆心,OF为半径作圆交双曲线的渐近线于异于原点的两点A、B,若<0,则双曲线的离心率e的取值范围为( )
| A. | B. | (1,2) | C. | (2,+∞) | D. |
10.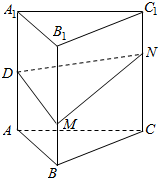 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )| A. | 平面DMN⊥平面BCC1B1 | |
| B. | 三棱锥A1-DMN的体积为定值 | |
| C. | △DMN可能为直角三角形 | |
| D. | 平面DMN与平面ABC所成的锐二面角范围为(0,] |

 如图所示,ABFC-A1B1F1C1为正四棱柱,D为BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,BC1⊥AB1,BC1⊥A1C.求证:
如图所示,ABFC-A1B1F1C1为正四棱柱,D为BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,BC1⊥AB1,BC1⊥A1C.求证: 如图,点E,F分别在正方体ABCD-A1B1C1D1的棱DD1、AB上,下列命题:
如图,点E,F分别在正方体ABCD-A1B1C1D1的棱DD1、AB上,下列命题: