若直线y=3x上存在点(x.y)满足约束条件$\left\{\begin{array}{l}{x+y+4≥0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$.则实数m的取值范围是[-1.+∞)．题目和参考答案——青夏教育精英家教网—

题目内容

13．若直线y=3x上存在点（x，y）满足约束条件$\left\{\begin{array}{l}{x+y+4≥0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$，则实数m的取值范围是[-1，+∞）．

分析由约束条件作出可行域，在平面直角坐标系中画出直线y=3x，求得直线y=3x与直线x+y+4=0交点的横坐标得答案．

解答解：由约束条件$\left\{\begin{array}{l}{x+y+4≥0}\\{2x-y+8≥0}\\{x≤m}\end{array}\right.$作出可行域如图，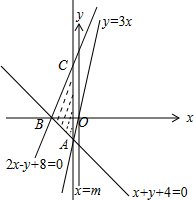

由图可知，只有当m大于等于直线y=3x与直线x+y+4=0交点的横坐标时满足条件．
联立$\left\{\begin{array}{l}{y=3x}\\{x+y+4=0}\end{array}\right.$，解得x=-1，y=-3．
∴实数m的取值范围是[-1，+∞）．
故答案为：[-1，+∞）．

点评本题考查简单的线性规划，考查数形结合的解题思想方法，是中档题．

练习册系列答案

暑假学习乐园浙江科学技术出版社系列答案

新暑假作业浙江教育出版社系列答案

小升初衔接教程快乐假期系列答案

轻松暑假总复习系列答案

书屯文化期末暑假期末冲刺假期作业云南人民出版社系列答案

4．设函数f（x）=（x+1）²ln（x+1）+bx，曲线y=f（x）在点（0，0）处的切线方程为y=0．
（Ⅰ）求b的值；
（Ⅱ）证明：当x≥0时，f（x）≥$\frac{3}{2}{x^2}$；
（Ⅲ）若当x≥0时，f（x）≥mx²恒成立，求实数m的取值范围．

1．已知命题P：?b∈（-∞，2），f（x）=x²+bx+c在（-∞，-1）上为减函数；命题Q：?x₀∈Z，使得2${\;}^{{x}_{0}}$＜1．则在命题￢P∨￢Q，￢P∧￢Q，P∨￢Q，P∧￢Q中任取一个命题，则取得真命题的概率是$\frac{1}{4}$．

8．

如图，边长为2的正方形ABCD是圆柱的中截面，点E为线段BC的中点，点S为圆柱的下底面圆周上异于A，B的一个动点．
（1）在圆柱的下底面上确定一定点F，使得EF∥平面ASC；
（2）求证：平面ASC⊥平面BSC．

18．在一次数学测试（满分为150分）中，某校2000名考生的分数X近似服从正态分布N（100，σ²）．据统计，分数在100～110分段的考生共440人，估计分数在90分以上的考生大概有（　　）人．

5．已知实数x，y满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{3x-y-3≤0}\end{array}\right.$，则|x-2y-1|的取值范围是[0，5]．

2．已知x，y满足约束条件$\left\{\begin{array}{l}x＜0\\ y＞0\\ x+y-2≤0\\ x-y+4≥0\end{array}\right.$，若目标函数z=x+my（m≠0）取得最大值时最优解有无数个，则m的值为1．

3．某单位要从甲、乙、丙、丁四支门球队中选拔两支参加上级比赛，选拔赛采用单循环制（即每两个队比赛一场），并规定积分前两名的队出线，其中胜一场积3分，平一场积1分，负一场积0分．在经过三场比赛后，目前的积分状况如下：甲队积7分，乙队积1分，丙和丁队各积0分．根据以往的比赛情况统计：

	乙队胜的概率	乙队平的概率	乙队负的概率
与丙队比赛	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{2}$
与丁队比赛	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$

注：各队之间比赛结果相互独立．
（Ⅰ）选拔赛结束，求乙队积4分的概率；
（Ⅱ）设随机变量X为选拔赛结束后乙队的积分，求随机变量X的分布列与数学期望；
（Ⅲ）在目前的积分情况下，M同学认为：乙队至少积4分才能确保出线，N同学认为：乙队至少积5分才能确保出线．你认为谁的观点对？或是两者都不对？（直接写结果，不需证明）

试题分类