题目内容
9.假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如图所示:横轴为投资时间,纵轴为回报,根据以上信息,若使回报最多,下列说法错误的是( )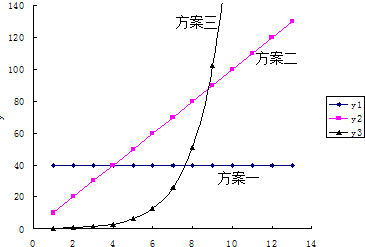
| A. | 投资3天以内(含3天),采用方案一 | B. | 投资4天,不采用方案三 | ||
| C. | 投资6天,采用方案二 | D. | 投资10天,采用方案二 |
分析 观察图象即可得到结论.
解答 解:由图可以看出,从每天回报看,在第一天到第三天,方案一最多,故A正确;
在第四天,方案一、二一样多,方案三最少,故B正确;
在第五天到第八天,方案二最多,故C正确;
第九天开始,方案三比其他两个方案所得回报多得多,故D不正确;
故选:D.
点评 本题考查函数模型的选择,考查数形结合的数学思想,考查学生分析解决问题的能力.

练习册系列答案
相关题目
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
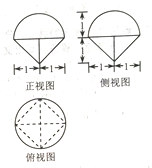

| A. | $\frac{2}{3}({π+1})$ | B. | $\frac{4}{3}$(π+1) | C. | $\frac{4}{3}$(π+$\frac{1}{2}$) | D. | $\frac{2}{3}$(π+$\frac{1}{2}$) |
14.如果函数y=|cos(ωx+$\frac{π}{4}$)|的图象关于直线x=π对称,则正实数ω的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
18.在一次数学测试(满分为150分)中,某校2000名考生的分数X近似服从正态分布N(100,σ2).据统计,分数在100~110分段的考生共440人,估计分数在90分以上的考生大概有( )人.
| A. | 560 | B. | 880 | C. | 1120 | D. | 1440 |
19.定义在实数集R上的函数y=f(x)的图象是连续不断的,对任意实数x,若存在实常数t使得f(t+x)=-tf(x)恒成立,则称f(x)是一个“t型函数”.在下列关于“t型函数”的四个命题中,其中真命题是( )
| A. | f(x)=0是常值函数中唯一一个“t型函数” | |
| B. | f(x)=x2是一个“t型函数” | |
| C. | f(x)=|x-$\frac{1}{2}$|是一个“t型函数” | |
| D. | “$\frac{1}{2}$型函数”至少有一个零点 |