题目内容
16.已知O为坐标原点,双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的右焦点F,以F为圆心,OF为半径作圆交双曲线的渐近线于异于原点的两点A、B,若$(\overrightarrow{AO}+\overrightarrow{AF})•\overrightarrow{OF}$<0,则双曲线的离心率e的取值范围为( )| A. | $(1,\sqrt{2})$ | B. | (1,2) | C. | (2,+∞) | D. | $({1,\frac{1}{2}})$ |
分析 如图,设OF的中点为M,则$(\overrightarrow{AO}+\overrightarrow{AF})•\overrightarrow{OF}<0$等价于$({2\overrightarrow{AM}})•({2\overrightarrow{MF}})<0?\overrightarrow{MA}•\overrightarrow{MF}>0?0<∠AMF<\frac{π}{2}$,也就是要求点A的横坐标${x_A}>\frac{c}{2}$,求出点A的横坐标,即可求出双曲线的离心率e的取值范围.
解答 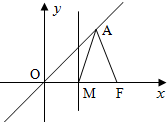 解:取M为OF中点,则$(\overrightarrow{AO}+\overrightarrow{AF})•\overrightarrow{OF}<0$等价于$({2\overrightarrow{AM}})•({2\overrightarrow{MF}})<0?\overrightarrow{MA}•\overrightarrow{MF}>0?0<∠AMF<\frac{π}{2}$.
解:取M为OF中点,则$(\overrightarrow{AO}+\overrightarrow{AF})•\overrightarrow{OF}<0$等价于$({2\overrightarrow{AM}})•({2\overrightarrow{MF}})<0?\overrightarrow{MA}•\overrightarrow{MF}>0?0<∠AMF<\frac{π}{2}$.
也就是要求点A的横坐标${x_A}>\frac{c}{2}$.
由$\left\{\begin{array}{l}{(x-c)^2}+{y^2}={c^2}\\ y=\frac{b}{a}x\end{array}\right.$
解得${x_A}=\frac{{2{a^2}}}{c}$,故需$\frac{{2{a^2}}}{c}>\frac{c}{2}$,解得e<2,则e∈(1,2).
故选:B.
点评 本题考查了双曲线的标准方程与简单几何性质等知识,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
6.已知sinα+cos(π-α)=$\frac{1}{3}$,则sin2α的值为( )
| A. | $\frac{8}{9}$ | B. | $\frac{1}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{4}{9}$ |
7.在某学校组织的一次利于定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次.某同学在A处的命中率q1为$\frac{1}{4}$,在B处的命中率为q2.该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为:
(I)求q2的值;
(Ⅱ)求随机变量ξ的数学期望.
| ξ | 0 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{25}$ | p1 | p2 | p3 | p4 |
(Ⅱ)求随机变量ξ的数学期望.
6.已知集合A={-2,3},B={x|x≤2},U=A∪B,则∁U(A∩B)=( )
| A. | {3} | B. | {x|x≤2,或x=3} | ||
| C. | {x|x<-2或-2<x≤2,或x=3} | D. | {x|x<-2,或-2<x≤2} |
 如图,边长为2的正方形ABCD是圆柱的中截面,点E为线段BC的中点,点S为圆柱的下底面圆周上异于A,B的一个动点.
如图,边长为2的正方形ABCD是圆柱的中截面,点E为线段BC的中点,点S为圆柱的下底面圆周上异于A,B的一个动点.