题目内容
10．
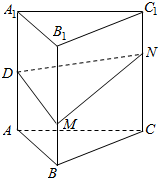如图，正三棱柱ABC-A1B1C1（底面是正三角形，侧棱垂直底面）的各条棱长均相等，D为AA1的中点．M、N分别是BB1、CC1上的动点（含端点），且满足BM=C1N．当M，N运动时，下列结论中不正确的是（ ）| A． | 平面DMN⊥平面BCC1B1 | |
| B． | 三棱锥A1-DMN的体积为定值 | |
| C． | △DMN可能为直角三角形 | |
| D． | 平面DMN与平面ABC所成的锐二面角范围为（0，$\frac{π}{4}$] |
分析 由BM=C1N，得线段MN必过正方形BCC1B1的中心O，由DO⊥平面BCC1B1，可得平面DMN⊥平面BCC1B1；
由△A1DM的面积不变，N到平面A1DM的距离不变，得到三棱锥A1-DMN的体积为定值；
利用反证法思想说明△DMN不可能为直角三角形；
平面DMN与平面ABC平行时所成角为0，当M与B重合，N与C1重合时，平面DMN与平面ABC所成的锐二面角最大．
解答 解：如图，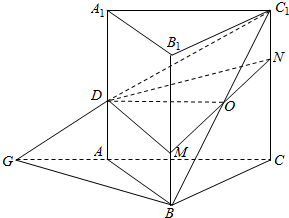
当M、N分别在BB1、CC1上运动时，若满足BM=C1N，则线段MN必过正方形BCC1B1的中心O，而DO⊥平面BCC1B1，∴平面DMN⊥平面BCC1B1，A正确；
当M、N分别在BB1、CC1上运动时，△A1DM的面积不变，N到平面A1DM的距离不变，∴棱锥N-A1DM的体积不变，即三棱锥A1-DMN的体积为定值，B正确；
若△DMN为直角三角形，则必是以∠MDN为直角的直角三角形，但MN的最大值为BC1，而此时DM，DN的长大于BB1，∴△DMN不可能为直角三角形，C错误；
当M、N分别为BB1，CC1中点时，平面DMN与平面ABC所成的角为0，当M与B重合，N与C1重合时，平面DMN与平面ABC所成的锐二面角最大，为∠C1BC，等于$\frac{π}{4}$．
∴平面DMN与平面ABC所成的锐二面角范围为（0，$\frac{π}{4}$]，D正确．
故选：C．
点评 本题考查了命题的真假判断与应用，考查了棱柱的结构特征，考查了空间想象能力和思维能力，是中档题．
练习册系列答案
通城学典默写能手系列答案
相关题目
18．在一次数学测试（满分为150分）中，某校2000名考生的分数X近似服从正态分布N（100，σ2）．据统计，分数在100～110分段的考生共440人，估计分数在90分以上的考生大概有（ ）人．
| A． | 560 | B． | 880 | C． | 1120 | D． | 1440 |
19．定义在实数集R上的函数y=f（x）的图象是连续不断的，对任意实数x，若存在实常数t使得f（t+x）=-tf（x）恒成立，则称f（x）是一个“t型函数”．在下列关于“t型函数”的四个命题中，其中真命题是（ ）
| A． | f（x）=0是常值函数中唯一一个“t型函数” | |
| B． | f（x）=x2是一个“t型函数” | |
| C． | f（x）=|x-$\frac{1}{2}$|是一个“t型函数” | |
| D． | “$\frac{1}{2}$型函数”至少有一个零点 |