题目内容
6. 如图所示,ABFC-A1B1F1C1为正四棱柱,D为BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,BC1⊥AB1,BC1⊥A1C.求证:
如图所示,ABFC-A1B1F1C1为正四棱柱,D为BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,BC1⊥AB1,BC1⊥A1C.求证:(Ⅰ)平面A1BD1∥平面AC1D;
(Ⅱ)BC1⊥B1D.
分析 (Ⅰ)根据面面平行的判定定理进行证明平面A1BD1∥平面AC1D;
(Ⅱ)根据线面垂直的性质定理即可证明BC1⊥B1D.
解答 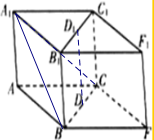 证明:(Ⅰ)∵A1B∥平面AC1D,
证明:(Ⅰ)∵A1B∥平面AC1D,
∴设A1C的中点为E,
则平面A1BC∩平面AC1D=ED,
∴A1B∥ED;
∵E是AC1的中点,
∴D是BC的中点,
即BDC1D1为平行四边形,
∴BD1∥DC1,A1D1∥AD,
∵BD1,A1D1?平面A1BD1,AD?平面AC1D,
∴平面A1BD1∥平面AC1D;
(Ⅱ)∵BC1⊥AB1,BC1⊥AC1,
∴BC1⊥FB1,
∵AB1∩B1F=B1,
∴BC1⊥平面AB1F,
∵DB1?平面AB1F,
∴BC1⊥B1D.
点评 本题主要考查面面平行和线面垂直性质定理的应用,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
相关题目
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
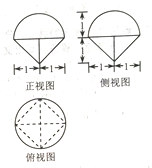

| A. | $\frac{2}{3}({π+1})$ | B. | $\frac{4}{3}$(π+1) | C. | $\frac{4}{3}$(π+$\frac{1}{2}$) | D. | $\frac{2}{3}$(π+$\frac{1}{2}$) |
14.如果函数y=|cos(ωx+$\frac{π}{4}$)|的图象关于直线x=π对称,则正实数ω的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为 4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
18.在一次数学测试(满分为150分)中,某校2000名考生的分数X近似服从正态分布N(100,σ2).据统计,分数在100~110分段的考生共440人,估计分数在90分以上的考生大概有( )人.
| A. | 560 | B. | 880 | C. | 1120 | D. | 1440 |
16.抛物线y=ax2(a<0)的准线方程是( )
| A. | y=-$\frac{1}{2a}$ | B. | y=-$\frac{1}{4a}$ | C. | y=$\frac{1}{2a}$ | D. | y=$\frac{1}{4a}$ |