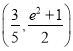题目内容
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() 和
和![]() ,离心率是
,离心率是![]() ,直线
,直线![]() 过点
过点![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,
时, ![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当直线![]() 绕点
绕点![]() 运动时,试求
运动时,试求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)椭圆![]() 的标准方程为
的标准方程为![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)由题意结合椭圆的定义可知![]() 的周长为
的周长为![]()
![]() ,
, ![]() ,结合离心率可知
,结合离心率可知![]() ,
, ![]() ,则椭圆
,则椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)设![]() ,
, ![]() 两点坐标分别为
两点坐标分别为![]() ,
, ![]() ,当直线
,当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() ,当直线
,当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() ,当直线
,当直线![]() 斜率为
斜率为![]() 时,
时, ![]() ,当直线
,当直线![]() 斜率存在且不为
斜率存在且不为![]() 时,联立直线方程与椭圆方程可得
时,联立直线方程与椭圆方程可得![]() ,则
,则![]() ,
, ![]() ,结合韦达定理整理计算可得不等式
,结合韦达定理整理计算可得不等式![]() ,解得
,解得![]() ,则
,则![]() .
.
试题解析:
(Ⅰ)∵![]() 的周长为
的周长为![]()
![]()
![]() ,
,
∴![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)设![]() ,
, ![]() 两点坐标分别为
两点坐标分别为![]() ,
, ![]() ,
,
当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() 点与上顶点重合时,
点与上顶点重合时, ![]() ,
,
当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() 点与下顶点重合时,
点与下顶点重合时, ![]() ,
,
当直线![]() 斜率为
斜率为![]() 时,
时, ![]() ,
,
当直线![]() 斜率存在且不为
斜率存在且不为![]() 时,不妨设直线
时,不妨设直线![]() 方程为
方程为![]() ,
,
联立![]() ,
,
得![]() ,
,
则有![]() ,①
,①
![]() ②
②
设![]() ,则
,则![]() ,代入①②得
,代入①②得
![]() ③
③
![]() ④
④
∴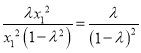
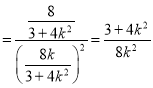
![]() ,
,
即![]() ,解得
,解得![]() ,
,
综上, ![]()

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
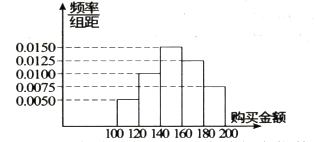
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.