题目内容
【题目】已知函数f(x)=xlnx和g(x)=m(x2-1)(m∈R).
(1)m=1时,求方程f(x)=g(x)的实根;
(2)若对任意的x∈(1,+∞),函数y=g(x)的图象总在函数y=f(x)图象的上方,求m的取值范围;
(3)求证: ![]() +
+![]() +…+
+…+![]() >ln(2n+1) (n∈N*).
>ln(2n+1) (n∈N*).
【答案】(1)见解析(2) ![]() .(3) 见解析
.(3) 见解析
【解析】试题分析:(1)代入![]() 时,
时, ![]() ,即
,即![]() ,整理方程得
,整理方程得![]() ,利用导数判断函数的单调性为递减函数,故最多有一个零点,而
,利用导数判断函数的单调性为递减函数,故最多有一个零点,而![]() ,故方程
,故方程![]() 有唯一的实根
有唯一的实根![]() ;(2)对于任意的
;(2)对于任意的![]() ,
, ![]() 恒成立,通过构造函数
恒成立,通过构造函数![]() ,利用导函数判断函数的单调性,
,利用导函数判断函数的单调性, ![]() ,通过讨论
,通过讨论![]() ,判断是否符合题意;(3)由(2)知,当
,判断是否符合题意;(3)由(2)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立,结合题型,构造不妨令
成立,结合题型,构造不妨令![]() ,得出
,得出![]() ,利用累加可得结论.
,利用累加可得结论.
试题解析:(1) ![]() 时,
时, ![]() ,即
,即![]() ,而
,而![]() ,所以方程即为
,所以方程即为![]() .
.
令![]() ,则
,则![]() ,而
,而![]() ,故方程
,故方程![]() 有唯一的实根
有唯一的实根![]() .
.
(2)对于任意的![]() ,函数
,函数![]() 的图象总在函数
的图象总在函数![]() 图象的上方,
图象的上方,
即![]() ,
, ![]() ,即
,即![]() ,
,
设![]() ,即
,即![]() ,
, ![]() ,则
,则![]()
①若![]() ,则
,则![]() ,
, ![]() ,这与题设
,这与题设![]() 矛盾.
矛盾.
若![]() ,方程
,方程![]() 的判别式
的判别式![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]()
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即不等式成立.
,即不等式成立.
当![]() ,即
,即![]() 时,方程
时,方程![]() 有两个实根,设两根为
有两个实根,设两根为![]() ,
, ![]() 且
且![]() ,则
,则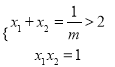
∴方程有两个正实根且![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增, ![]() 与题设矛盾.
与题设矛盾.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
(3)证明 由(2)知,当![]() 时,
时, ![]() 时,
时, ![]() 成立.
成立.
不妨令![]()
∴![]() ,即
,即
![]()
∴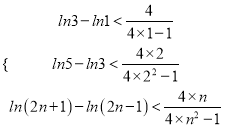 ,累加可得
,累加可得![]()

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目