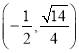题目内容
【题目】已知椭圆![]() :
:![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且过点
的焦点重合,且过点![]() .过点
.过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 为椭圆的左顶点.
为椭圆的左顶点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直线l的方程为x=1.
;(2)直线l的方程为x=1.
【解析】试题分析:(1)利用椭圆和抛物线有一个公共焦点和点在椭圆上进行求解;(2) 联立直线和椭圆的方程,得到关于![]() 的一元二次方程,再利用根与系数的关系、弦长公式和基本不等式进行求解.
的一元二次方程,再利用根与系数的关系、弦长公式和基本不等式进行求解.
试题解析:(1)因为抛物线y2=4![]() x的焦点为(
x的焦点为(![]() ,0),所以椭圆C的半焦距c=
,0),所以椭圆C的半焦距c=![]() ,即a2-b2=3. ①
,即a2-b2=3. ①
把点Q![]() 代入
代入![]() +
+![]() =1,得
=1,得![]() +
+![]() =1. ②
=1. ②
由①②解得a2=4,b2=1.所以椭圆C的标准方程为![]() +y2=1.
+y2=1.
(2)设直线l的方程为x=ty+1,代入![]() +y2=1,
+y2=1,
得(t2+4)y2+2ty-3=0.
设M(x1,y1),N(x2,y2),则有y1+y2=-![]() ,y1y2=-
,y1y2=-![]() .
.
则|y1-y2|=![]() =
=![]() =
=![]() =
=![]() =
=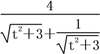 .令
.令![]() =m(m≥
=m(m≥![]() ).易知函数y=m+
).易知函数y=m+![]() 在[
在[![]() ,+∞)上单调递增,
,+∞)上单调递增,
则![]() +
+![]() ≥
≥![]() +
+![]() =
=![]() ,当且仅当m=
,当且仅当m=![]() ,即t=0时,取等号.
,即t=0时,取等号.
所以|y1-y2|≤![]() .所以△AMN的面积S=
.所以△AMN的面积S=![]() |AP||y1-y2|≤
|AP||y1-y2|≤![]() ×3×
×3×![]() =
=![]() ,
,
所以Smax=![]() ,此时直线l的方程为x=1.
,此时直线l的方程为x=1.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目