题目内容
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点.
(1)求证:DE∥平面PFB;
(2)已知二面角P-BF-C的余弦值为 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积. 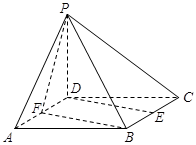
(1)求证:DE∥平面PFB;
(2)已知二面角P-BF-C的余弦值为
 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积. 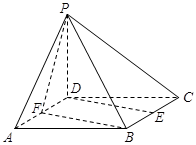
(Ⅰ)因为E,F分别为正方形ABCD的两边BC,AD的中点,
所以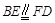 , 2分
, 2分
所以,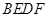 为平行四边形, 3分
为平行四边形, 3分
得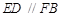 , 4分
, 4分
又因为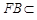 平面PFB,且
平面PFB,且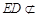 平面PFB, 所以DE∥平面PFB. 5分
平面PFB, 所以DE∥平面PFB. 5分
(Ⅱ)如图,以D为原点,射线DA,DC,DP分

别为x,y,z轴建立空间直角坐标系. 6分
设PD=a, 可得如下点的坐标:
P(0,0,a),F(1,0,0),B(2,2,0) 则有: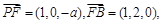
因为PD⊥底面ABCD,所以平面ABCD的一个法向量为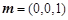 , 7分
, 7分
设平面PFB的一个法向量为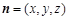 ,则可得
,则可得
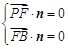 即
即 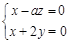
令x=1,得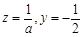 ,所以
,所以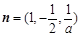 . 8分
. 8分
由已知,二面角P-BF-C的余弦值为 ,所以得:
,所以得:
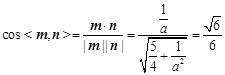 ,
,
解得a =2. 因为PD是四棱锥P-ABCD的高,所以,其体积为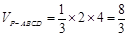 .
.
所以
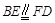 , 2分
, 2分所以,
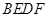 为平行四边形, 3分
为平行四边形, 3分得
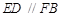 , 4分
, 4分 又因为
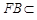 平面PFB,且
平面PFB,且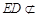 平面PFB, 所以DE∥平面PFB. 5分
平面PFB, 所以DE∥平面PFB. 5分(Ⅱ)如图,以D为原点,射线DA,DC,DP分

别为x,y,z轴建立空间直角坐标系. 6分
设PD=a, 可得如下点的坐标:
P(0,0,a),F(1,0,0),B(2,2,0) 则有:
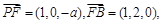
因为PD⊥底面ABCD,所以平面ABCD的一个法向量为
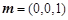 , 7分
, 7分设平面PFB的一个法向量为
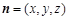 ,则可得
,则可得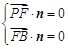 即
即 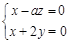
令x=1,得
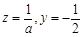 ,所以
,所以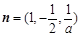 . 8分
. 8分由已知,二面角P-BF-C的余弦值为
 ,所以得:
,所以得: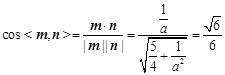 ,
, 解得a =2. 因为PD是四棱锥P-ABCD的高,所以,其体积为
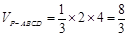 .
.(1)证:DE//BF即可;
(2)可以利用向量法根据二面角P-BF-C的余弦值为 ,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
(2)可以利用向量法根据二面角P-BF-C的余弦值为
 ,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
,确定高PD的值,即可求出四棱锥的体积.也可利用传统方法直接作出二面角的平面角,求高PD的值也可.在找平面角时,要考虑运用三垂线或逆定理.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 ,类比以上结论,则长、宽、高分别为
,类比以上结论,则长、宽、高分别为 的长方体的外接球半径为( )
的长方体的外接球半径为( )



 中,
中, ,
, ,则四棱锥
,则四棱锥 的体积为 ▲ cm3.
的体积为 ▲ cm3.
 的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则
的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则 的取值范围是 .
的取值范围是 . ,则以四个氢原子为顶点的这个正四面体的体积为( )
,则以四个氢原子为顶点的这个正四面体的体积为( )



 中,
中,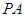 ^底面
^底面 ,若底面
,若底面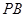
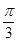 ,若
,若 是
是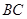 的中点,
的中点,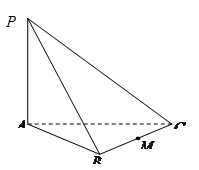
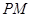 与
与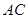 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
 ∥平面
∥平面 ;
; 平面
平面 ;
; 的四个顶点都在体积为
的四个顶点都在体积为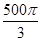 的球的表面上,平面
的球的表面上,平面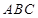 所在的小圆面积为
所在的小圆面积为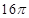 ,则该三棱锥的高的最大值是
,则该三棱锥的高的最大值是