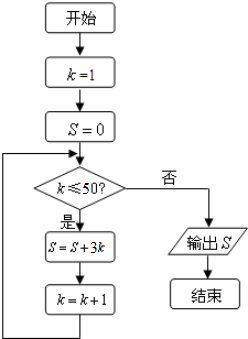
题目内容
2.已知$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(1,-1)(1)求$\overrightarrow{a}$-$\overrightarrow{b}$及|$\overrightarrow{a}$-$\overrightarrow{b}$|;
(2)若k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直,求实数k的值.
分析 (1)由条件利用两个向量坐标形式的运算法则求得$\overrightarrow{a}$-$\overrightarrow{b}$的坐标,可得|$\overrightarrow{a}$-$\overrightarrow{b}$|的值.
(2)由条件利用两个向量垂直的性质,求得实数k的值.
解答 解:(1)由$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(1,-1),可得$\overrightarrow{a}$-$\overrightarrow{b}$=(1,2),
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{1+4}$=$\sqrt{5}$.
(2)由题意可得k$\overrightarrow{a}$+$\overrightarrow{b}$=(2k+1,k-1),$\overrightarrow{a}$-$\overrightarrow{b}$=(1,2),
再由k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直,可得(k$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=(2k+1,k-1)•(1,2)
=2k+1+2(k-1)=4k-1=0,
∴k=$\frac{1}{4}$.
点评 本题主要考查两个向量的数量积公式,两个向量坐标形式的运算,两个向量垂直的性质,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
12.已知角α的终边经过点P(-b,4)且cosα=-$\frac{3}{5}$,则b的值等于( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 5 |
7.定义:$\frac{n}{{p}_{1}+{p}_{1}+…+{p}_{n}}$为n个p1,p2,…pn的“均倒数”,若已知正数数列{an}的前n项的”均倒数“为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}-1}{2}$.,$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$=( )
| A. | $\frac{2013}{4027}$ | B. | $\frac{4026}{4027}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{4028}{4029}$ |
14.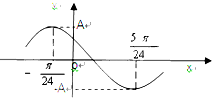 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )| A. | -$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | -1+$\sqrt{3}$ |
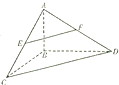 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,AB=3,BC=BD=4,点E,F分别是AC,AD的中点