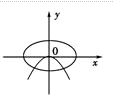
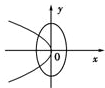
题目内容
20.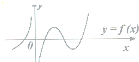 已知函数y=f(x)在定义域内可导,且图象如图所示,则此导函数y=f′(x)的图象可知为图中的( )
已知函数y=f(x)在定义域内可导,且图象如图所示,则此导函数y=f′(x)的图象可知为图中的( )| A. | 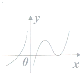 | B. |  | C. | 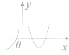 | D. |  |
分析 利用导数与函数的单调性的关系即可得出.
解答 解:当x<0时,由函数y=f(x)图象可知:函数f(x)单调递增,因此f′(x)>0;
同理可得x>0时函数f(x)的单调性:先增后减再增,于是导函数满足:f′(x)>0,f′(x)<0,f′(x)>0,可得:只有D满足条件.
故选:D.
点评 本题考查了导数与函数的单调性的关系,考查了数形结合的思想方法与推理能力,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
8.已知x>0,y>0,且2x+y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值是( )
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
15.已知等差数列{an}中,a2+a6=16,则a4=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
5.一个几何体的三视图如图所示,则该几何体可以是( )
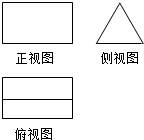

| A. | 棱锥 | B. | 棱台 | C. | 圆锥 | D. | 棱柱 |
12.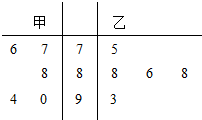 在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
 在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )| A. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,乙比甲成绩稳定 | B. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,甲比乙成绩稳定 | ||
| C. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,乙比甲成绩稳定 |
19.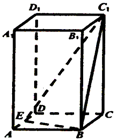 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | $\frac{4}{3}$ | D. | 8 |
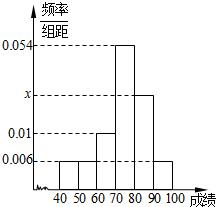 某班50位学生期中考试数学成绩的频率分布直方图如图所示.
某班50位学生期中考试数学成绩的频率分布直方图如图所示.