题目内容
9.数列{an}中,a1=1,前n项和为Sn,且an+1=2Sn(n∈N*)(1)求an;
(2)求Tn=a1+2a2+3a3+…+nan.
分析 (1)根据数列an与Sn的关系进行求解即可.
(2)利用错位相减法即可求Tn=a1+2a2+3a3+…+nan.
解答 解:(1)∵an+1=2Sn=Sn+1-Sn,
∴3Sn=Sn+1,
即$\frac{{S}_{n+1}}{{S}_{n}}$=3,
则{Sn}是以公比q=3的等比数列,首项为S1=a1=1,
则Sn=3n-1,
则当n≥2时,an=Sn-Sn-1=3n-1-3n-2=2•3n-2,
当n=1时,a1=1不满足an=2•3n-2,
∴an=$\left\{\begin{array}{l}{1,}&{n=1}\\{2•{3}^{n-2},}&{n≥2}\end{array}\right.$
(2)∵Tn=a1+2a2+3a3+…+nan.
∴3Tn=3a1+2•3a2+3•3a3+…+n•3an=3a1+2a3+3a4+…+n•3an+1,
则两式相减得2Tn=2a1-2a2-a3-…-an+n•3an+1
=2-4-(a3+…+an)+n•2•3n-1,
=-2-$\frac{6(1-{3}^{n-2})}{1-3}$)+n•2•3n-1
=-2-3(1-3n-2)+n•2•3n-1
=-5+(2n-1)•3n-1
当n=1时,Tn=a1+2a2+3a3+…+nan=a1=1,
故Tn=$\left\{\begin{array}{l}{1,}&{n=1}\\{-5+(2n-1)•{3}^{n-1},}&{n≥2}\end{array}\right.$
点评 本题主要考查数列通项公式的求解以及前n项和的计算,利用错位相减法是解决本题的关键.

练习册系列答案
相关题目
1.在△ABC中,sin2A=sinBsinC,∠A=$\frac{π}{3}$,则∠B等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
8.已知集合A={x|log3(x2-2x)>1},B={x∈N|x<5},则( )
| A. | A∩B=(3,5) | B. | A∪B=5 | C. | A∪B={x|x≤5} | D. | A∩B={4} |
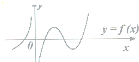 已知函数y=f(x)在定义域内可导,且图象如图所示,则此导函数y=f′(x)的图象可知为图中的( )
已知函数y=f(x)在定义域内可导,且图象如图所示,则此导函数y=f′(x)的图象可知为图中的( )