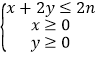题目内容
【题目】某公司一年经销某种商品，年销售量400吨，每吨进价5万元，每吨销售价8万元．全年进货若干次，每次都购买x吨，运费为每次2万元，一年的总存储费用为2x万元．
（1）求该公司经销这种商品一年的总利润y与x的函数关系；
（2）要使一年的总利润最大，则每次购买量为多少？并求出最大利润．
【答案】
（1）解：某公司一年购买某种货物400吨，每次都购买x吨，则需要购买 
次，运费为2万元/次，一年的总存储费用为2x万元，一年的总运费与总存储费用之和为 2+2x万元．
∴该公司经销这种商品一年的总利润y与x的函数关系y=1200﹣（ 2+2x）
（2）解：要使一年的总利润最大，只要一年的总运费与总存储费用之和最小．
∵ 2+2x≥80，当 2=2x即x=20吨时，等号成立．
∴每次购买20吨时，一年的总运费与总存储费用之和最小，最大利润1120万元
【解析】（1）先设某公司每次都购买x吨，由于一年购买某种货物400吨，得出需要购买的次数，从而求得一年的总运费与总存储费用之和，即可求出该公司经销这种商品一年的总利润y与x的函数关系；（2）利用基本不等式求得一年的总运费与总存储费用之和最小即可．
练习册系列答案
相关题目
