��Ŀ����
����Ŀ��ijѧϰ��ȤС�鿪չ��ѧ�����ijɼ�������ɼ��Ĺ�ϵ���Ŀ����о��������У�߶��꼶800��ѧ����ѧ����ĩ�����ĺ�����ɼ������Ƿ��������ý�������ĺ�����ɼ����������60�ˣ����ijɼ����㵫����ɼ����������140�ˣ�����ɼ����㵫���ijɼ����������100�ˣ�
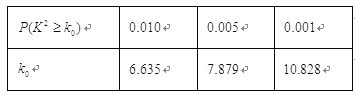
�����ܷ���![]() �İ�����Ϊ����Уѧ�����ijɼ�����������ɼ��Ƿ������й�ϵ����
�İ�����Ϊ����Уѧ�����ijɼ�����������ɼ��Ƿ������й�ϵ����
���������������õ���Ƶ����Ϊ���ʣ��Ӹ�У�߶��꼶ѧ���ɼ��У��зŻص������ȡ3��ѧ���ijɼ���������ȡ�ijɼ��У����ġ��������Ƴɼ�������һ�����������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() ��
��
����![]() .
.
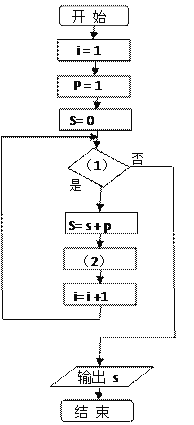
���𰸡�(1) ��![]() �İ���(2)������
����(2)������
�������������������1�����ݿ�����ʽ����![]() ������ο����ݱȽϵ��Ƿ��а��գ�2���зŻ��¼����ɿ���Ϊ�����ظ����飬������������Ӷ���ֲ�
������ο����ݱȽϵ��Ƿ��а��գ�2���зŻ��¼����ɿ���Ϊ�����ظ����飬������������Ӷ���ֲ�![]() �����ݶ���ֲ���ʽ��ֲ��м���ѧ����
�����ݶ���ֲ���ʽ��ֲ��м���ѧ����
����������⣺�������������������
�������� | ���IJ����� | �ܼ� | |
�������� | 60 | 100 | 160 |
���ﲻ���� | 140 | 500 | 640 |
�ܼ� | 200 | 600 | 800 |
��Ϊ![]() ����
����![]() ֪����
֪����![]() �İ�����Ϊ����Уѧ�����ijɼ�����������ɼ��Ƿ������й�ϵ����
�İ�����Ϊ����Уѧ�����ijɼ�����������ɼ��Ƿ������й�ϵ����
��������֪�ã������ȡ1��ѧ���������ġ��������Ƴɼ�������һ������ĸ�����![]() ������
������![]() ��
��![]() ��
��![]() ��
��
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��![]() ��
��

����Ŀ��ij�༶����һ��֪ʶ����������Ϊ�����;��������Ρ��ֽ���������ɼ����÷־�Ϊ����������Ϊ100�֣�����ͳ�ƣ��Ƴ�����Ƶ�ʷֲ�����
�����������Σ� | Ƶ���������� | Ƶ�� |
[60��70�� | �� | 0.16 |
[70��80�� | 22 | �� |
[80��90�� | 14 | 0.28 |
[90��100] | �� | �� |
�� �� | 50 | 1 |
��1�����Ƶ�ʷֲ����еĿո��ڽ����ֱ��д����Ӧ�ո���ŵĴ𰸣���
��2�������������£��μӾ�����ÿλͬѧ���οڴ�4��С�⣬���2�������ֹ���⣬�����һ�Ƚ������ǰ�����ⶼ������Ͳ��ٴ�����⡣ijͬѧ���������ÿ�����Եĸ���![]() ��ֵǡ����Ƶ�ʷֲ����в�����80�ֵ�Ƶ�ʵ�ֵ��ͬ��
��ֵǡ����Ƶ�ʷֲ����в�����80�ֵ�Ƶ�ʵ�ֵ��ͬ��
�����ͬѧǡ�ô���4��������һ�Ƚ��ĸ��ʣ�
�ڼǸ�ͬѧ�����д������Ϊ![]() ����
����![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������