题目内容
【题目】已知点(2,5)和(8,3)是函数y=﹣k|x﹣a|+b与y=k|x﹣c|+d的图象仅有的两个交点,那么a+b+c+d的值为
【答案】18
【解析】解:∵函数y=﹣k|x﹣a|+b与y=k|x﹣c|+d的图象交于两点(2,5),(8,3),
∴5=﹣k|2﹣a|+b ①
3=﹣k|8﹣a|+b ②
5=k|2﹣c|+d ③
3=k|8﹣c|+d ④
①﹣②得2=﹣k|2﹣a|+k|8﹣a|⑤
③﹣④得2=k|2﹣c|﹣k|8﹣c|⑥
⑤=⑥得|8﹣a|+|8﹣c|=|2﹣c|+|2﹣a|
即|8﹣a|﹣|2﹣a|+|8﹣c|﹣|2﹣c|=0
设f(x)=|8﹣x|﹣|2﹣x|,则f(a)+f(c)=0,
画出函数f(x)的图象,如图,其关于点A(5,0)成中心对称,
故点a与点c关于点A(5,0)成中心对称,
∴![]() (a+c)=5,
(a+c)=5,
∴a+c=10,
又∵函数y=﹣k|x﹣a|+b的对称轴为x=a,函数y=k|x﹣c|+d的对称轴为x=c,
∴2<a<8,2<c<8
②+③:8=﹣k(8﹣a)+b+k(c﹣2)+d,
∴b+d=8,
∴a+b+c+d=18
故答案为:18.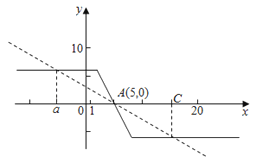
将两个交点代入函数y=﹣k|x﹣a|+b方程,得到方程组,将两个方程相减;据绝对值的意义及k的范围得到k,a满足的等式;同样的过程得到k,c满足的等式,两式联立求出a+c的值,再求出b+d,即可得到结论.

练习册系列答案
相关题目