题目内容
如图所示,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为______.
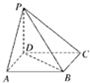

如图,以D为坐标原点,DA所在直线为x轴,DC所在线为y轴,DP所在线为z轴,建立空间坐标系,
∵点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,令PD=AD=1
∴A(1,0,0),P(0,0,1),B(1,1,0),D(0,0,0)
∴
=(1,0,-1),
=(-1,-1,0)
∴cosθ=
=
=-
故两向量夹角的余弦值为
,即两直线PA与BD所成角的度数为60°.
故答案为:60°
∵点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,令PD=AD=1
∴A(1,0,0),P(0,0,1),B(1,1,0),D(0,0,0)
∴
| PA |
| BD |
∴cosθ=
| ||||
|
|
| -1 | ||||
|
| 1 |
| 2 |
故两向量夹角的余弦值为
| 1 |
| 2 |
故答案为:60°

练习册系列答案
相关题目