题目内容
已知A、B、C是球O的球面上三点,∠BAC=90°,AB=2,BC=4,球O的表面积为48π,则异面直线AB与OC所成角余弦值为______.
设球O的半径为R,
则球O的表面积为S=4πR2=48π,解得R=2
.
∵AB=2,BC=4,∠BAC=90°,
∴BC为平面ABC截球所得小圆的直径,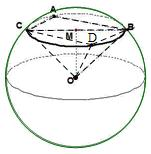
以AC、AB为邻边作平行四边形ACDB,可得四边形ACDB是截得小圆的内接矩形.
∵CD∥AB,∴∠OCD(或其补角)就是异面直线AB与OC所成角.
连线OD、OB,
△OCD中,CO=DO=R=2
,CD=AB=2.
∴cos∠OCD=
=
=
故答案为:
则球O的表面积为S=4πR2=48π,解得R=2
| 3 |
∵AB=2,BC=4,∠BAC=90°,
∴BC为平面ABC截球所得小圆的直径,

以AC、AB为邻边作平行四边形ACDB,可得四边形ACDB是截得小圆的内接矩形.
∵CD∥AB,∴∠OCD(或其补角)就是异面直线AB与OC所成角.
连线OD、OB,
△OCD中,CO=DO=R=2
| 3 |
∴cos∠OCD=
| CO2+CD2-DO2 |
| 2×CO×CD |
| 12+4+12 | ||
2×2
|
| ||
| 6 |
故答案为:
| ||
| 6 |

练习册系列答案
相关题目