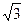题目内容
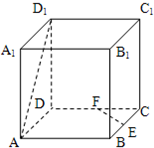
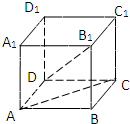
如图,在正方体ABCD-A1B1C1D1中,直线C1B与D1C所成角为( )
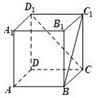

| A.30° | B.45° | C.60° | D.90° |
连接AC,D1A.
由正方体可得AB
C1D1,∴四边形ABC1D1是平行四边形.
∴BC1∥AD1.
∴∠AD1C或其补角是异面直线C1B与D1C所成角.
由正方体可得AC=CD1=D1A,
∴△ACD1是等边三角形,∴∠AD1C=60°.
∴异面直线C1B与D1C所成的角为60°.
故选C.
由正方体可得AB
| ∥ |
| . |
∴BC1∥AD1.
∴∠AD1C或其补角是异面直线C1B与D1C所成角.
由正方体可得AC=CD1=D1A,
∴△ACD1是等边三角形,∴∠AD1C=60°.
∴异面直线C1B与D1C所成的角为60°.
故选C.

练习册系列答案
相关题目
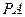 、
、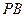 、
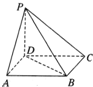
、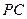 是从空间一点
是从空间一点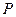 出发的三条射线,若
出发的三条射线,若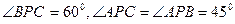 ,求二面角
,求二面角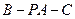 的大小.
的大小.
 B
B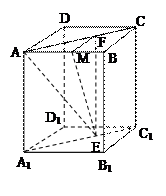 A.
A.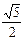 B.
B.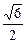 C.
C.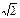 D.
D.