题目内容
(本小题满分14分)
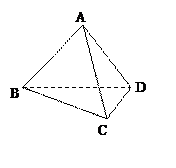
在四棱锥P—ABCD中,底面ABCD是一直角梯形,
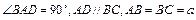 ,
,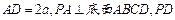 与底面成30°角.
与底面成30°角.
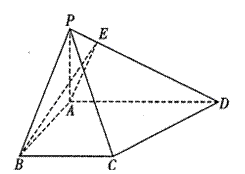
(1)若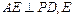 为垂足,求证:
为垂足,求证: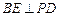 ;
;
(2)求平面PAB与平面PCD所成的锐二面角的余弦值.
在四棱锥P—ABCD中,底面ABCD是一直角梯形,
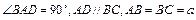 ,
,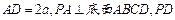 与底面成30°角.
与底面成30°角.
(1)若
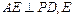 为垂足,求证:
为垂足,求证: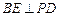 ;
;(2)求平面PAB与平面PCD所成的锐二面角的余弦值.
(1)略
(2)
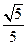
解法一:(1)
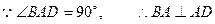
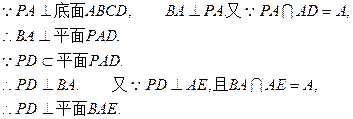
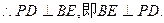 …………4分
…………4分延长AB与DC相交于G点,连PG,则面PAB
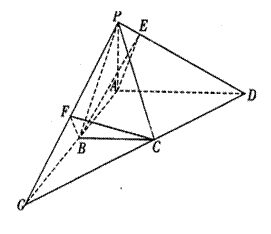
与面PCD的交线为PG,易知CB⊥平面PAB,过B作
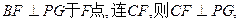
|
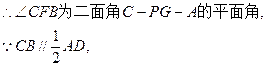
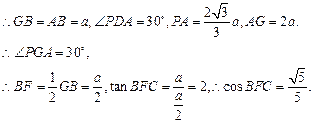
∴平面PAB与平面PCD所成
 的二面角的正切值为
的二面角的正切值为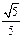 . ………14分
. ………14分解法二:
 (1)如图建立空间直角坐标系,
(1)如图建立空间直角坐标系,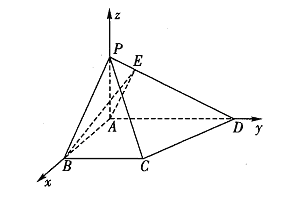
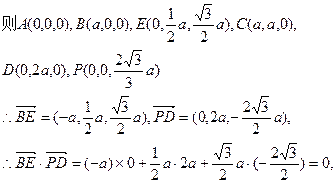
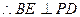
 …………4分
…………4分(2)易知,
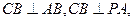
则
 的法向量。
的法向量。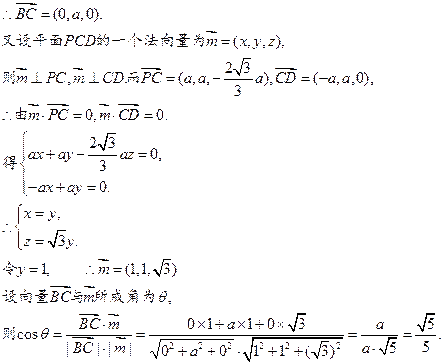
∴平面PAB与平面PCD所成锐二面角的余弦值为
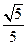 . …………14分
. …………14分
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 中,棱AB=BC=3,
中,棱AB=BC=3, =4,连结
=4,连结 , 在
, 在 上有点E,使得
上有点E,使得 ⊥平面EBD ,BE交
⊥平面EBD ,BE交
 所成角的大小;
所成角的大小;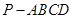 中,底面
中,底面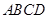 是直角梯形,
是直角梯形,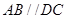 ,
,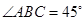 ,
,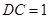 ,
,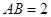 ,
,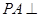 平面
平面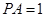 .
. 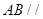 平面
平面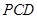 ;
;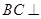 平面
平面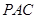 ;
; )如图,棱锥
)如图,棱锥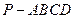 的底面
的底面 是矩形,
是矩形,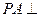 面
面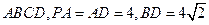 ,
,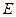 为
为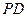 的中点.
的中点.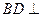 面
面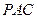 ;
; 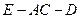 的余弦值;
的余弦值;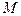 为
为 的中点,在棱
的中点,在棱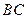 上是否存在点
上是否存在点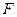 ,
,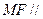 面
面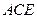 ?如果存在,请指出
?如果存在,请指出 点的位置;
点的位置;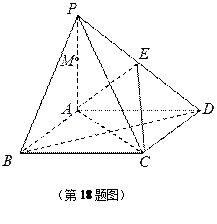
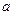 的
的 别是棱BB1、CC1、DD1的中点。
别是棱BB1、CC1、DD1的中点。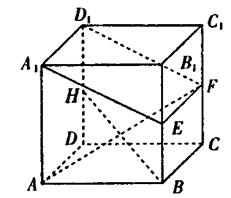
 中,
中,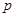 是侧面
是侧面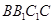 内一动点,若
内一动点,若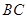 与直线
与直线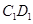 的距离相等,则动点
的距离相等,则动点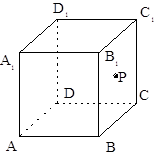
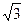 ,两个平面分别截球面得到两个圆⊙O1与⊙O2,若
,两个平面分别截球面得到两个圆⊙O1与⊙O2,若 视图中大三角形的边长是2的正三角形,俯视图为正六边形,那么该几何体的体积为 .
视图中大三角形的边长是2的正三角形,俯视图为正六边形,那么该几何体的体积为 .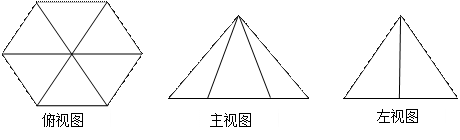
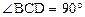 ,
,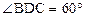 ,
,