题目内容
(本小题满分14分 )如图,棱锥
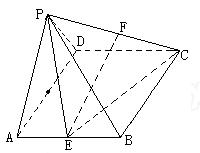
)如图,棱锥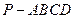 的底面
的底面 是矩形,
是矩形,
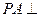 面
面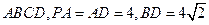 ,
,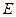 为
为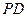 的中点.
的中点.
(1)求证: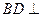 面
面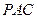 ;
;
(2)求二面角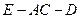 的余弦值;
的余弦值;
(3)设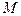 为
为 的中点,在棱
的中点,在棱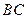 上是否存在点
上是否存在点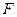 ,
,
使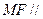 面
面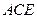 ?如果存在,请指出
?如果存在,请指出 点的位置;
点的位置;
如果不存在,请说明理由.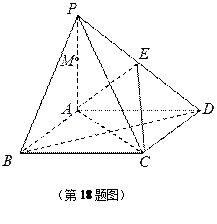
 )如图,棱锥
)如图,棱锥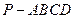 的底面
的底面 是矩形,
是矩形,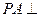 面
面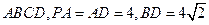 ,
,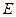 为
为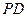 的中点.
的中点.(1)求证:
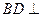 面
面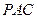 ;
; (2)求二面角
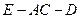 的余弦值;
的余弦值;(3)设
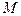 为
为 的中点,在棱
的中点,在棱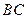 上是否存在点
上是否存在点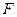 ,
,使
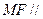 面
面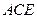 ?如果存在,请指出
?如果存在,请指出 点的位置;
点的位置;如果不存在,请说明理由.
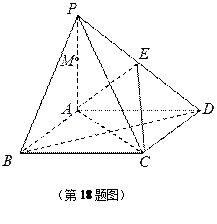
(1)略
(2)

(3)
 在棱
在棱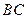 上存在点
上存在点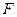 ,使
,使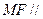 平面
平面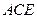 ,且
,且 为棱
为棱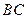 的中点
的中点证明:(1) 在

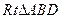 中,
中,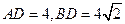 ,
,
 为正方形,因此
为正方形,因此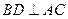 . ……………2分
. ……………2分∵
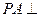 面
面 ,
, 面
面 ,
, . ……………3分
. ……………3分又
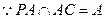
∴
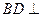 面
面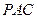 . ……………4分
. ……………4分解: (2) 建立如图所示的直角坐标系,则
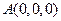 、
、 、
、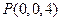 .………5分
.………5分 在
在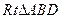 中,
中, ,
,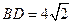 ,
,∴
 ,
, ,
, ,
, ∴
 ,
, .……6分
.……6分设面
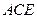 的法向量
的法向量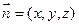 ,
,则
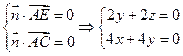 ,
,可以得到面
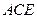 的一个法向量
的一个法向量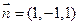 .
.  …………7分
…………7分又
 平面
平面 ,
,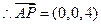 为面
为面
 的一个法向量, …………8分
的一个法向量, …………8分则
 ,
, 二面角
二面角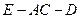 的余弦值为
的余弦值为 . …………10分
. …………10分(3)
 为
为 的中点,
的中点, 的坐标为
的坐标为 .
.设棱
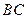 上存在点
上存在点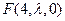 使
使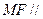 平面
平面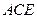 ,
, 则
 , …………11分
, …………11分由
 得面
得面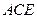 的一个法向量
的一个法向量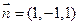 ,
, , …………13分
, …………13分 在棱
在棱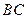 上存在点
上存在点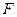 ,使
,使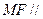 平面
平面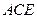 ,且
,且 为棱
为棱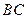 的中点.……14分
的中点.……14分
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
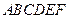 中,点
中,点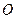 是矩形
是矩形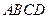 的对角线的交点,三角形
的对角线的交点,三角形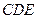 是等边三角形,棱
是等边三角形,棱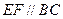 且
且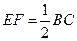 .
.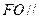 平面
平面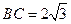 ,
,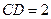 ,
, ,
, 与平面
与平面
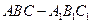 中, AB=1,
中, AB=1,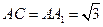 ,∠ABC=60
,∠ABC=60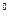 .
.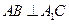 ;
;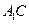 —B的余弦值。
—B的余弦值。 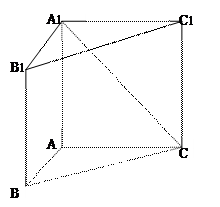
 所在的平面
所在的平面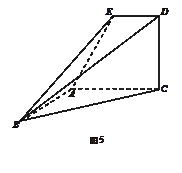
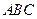 ,
,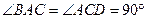 ,
,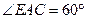 ,
,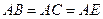 . (1)在直线
. (1)在直线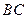 上是否存在一点
上是否存在一点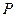 ,使得
,使得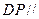 平面
平面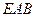 ?请证明你的结论;
?请证明你的结论;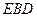 与平面
与平面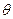 的余弦值。
的余弦值。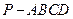 中,底面
中,底面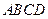 为正方形,
为正方形,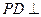 平面
平面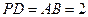 ,
,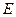 ,
,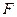 ,
,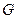 分别为
分别为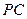 、
、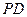 、
、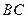 的中点.
的中点.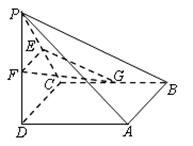
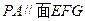 ;
;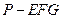 的体积.
的体积. 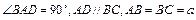 ,
,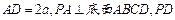 与底面成30°角.
与底面成30°角.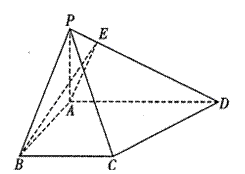
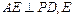 为垂足,求证:
为垂足,求证: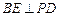 ;
;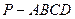 底面正方形的边长为4cm,高PO与斜高PE的夹角为
底面正方形的边长为4cm,高PO与斜高PE的夹角为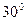 ,如图,求正四棱锥的表面积与体积
,如图,求正四棱锥的表面积与体积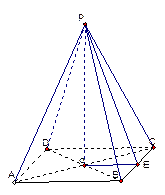
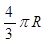 B.
B.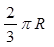 C.
C.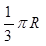 D.
D.