题目内容
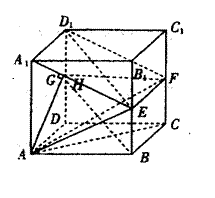
如图所示,在棱长为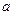 的
的
正方体ABCD—A1B1C1D1中,E、F、H分 别是棱BB1、CC1、DD1的中点。
别是棱BB1、CC1、DD1的中点。
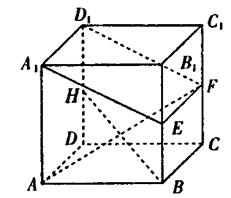
(Ⅰ)求证:BH//平面A1EFD1;
(Ⅱ)求直线AF与平面A1EFD1所成的角的正弦值。
 的
的正方体ABCD—A1B1C1D1中,E、F、H分
 别是棱BB1、CC1、DD1的中点。
别是棱BB1、CC1、DD1的中点。
(Ⅰ)求证:BH//平面A1EFD1;
(Ⅱ)求直线AF与平面A1EFD1所成的角的正弦值。
(Ⅰ)证明略
(Ⅱ)
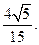
(Ⅰ)证明:连结D1E,
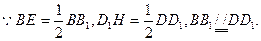
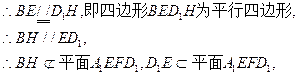
 ………………7分
………………7分
(Ⅱ)解:过A作AG⊥A1E,垂足为G。
∵A1D1⊥平面A1ABB1, ∴A1D1⊥AG,
∴A1D1⊥AG,
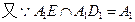 ∴AG⊥平面A1EFD1。
∴AG⊥平面A1EFD1。
连结FG,则∠AFG为所求的角。……9分

即直线AF与平面A1EFD1所成的角的正弦值为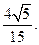 …………14分
…………14分

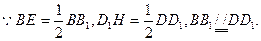
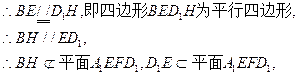
 ………………7分
………………7分(Ⅱ)解:过A作AG⊥A1E,垂足为G。
∵A1D1⊥平面A1ABB1,
 ∴A1D1⊥AG,
∴A1D1⊥AG,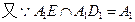 ∴AG⊥平面A1EFD1。
∴AG⊥平面A1EFD1。连结FG,则∠AFG为所求的角。……9分

即直线AF与平面A1EFD1所成的角的正弦值为
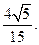 …………14分
…………14分
练习册系列答案
相关题目
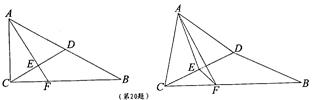
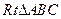 中,
中,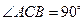 ,
,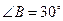 ,
,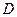 、
、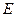 分别为
分别为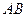 、
、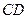 的中点,
的中点,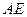 的延长线交
的延长线交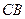 于
于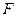 。现将
。现将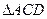 沿
沿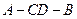 ,连接
,连接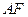 .
. :平面
:平面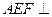 平面
平面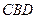 ;
;
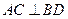 时,求二面角
时,求二面角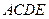 所在的平面
所在的平面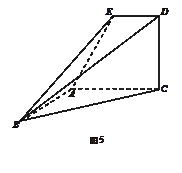
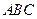 ,
,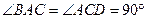 ,
,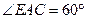 ,
,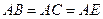 . (1)在直线
. (1)在直线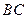 上是否存在一点
上是否存在一点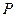 ,使得
,使得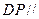 平面
平面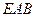 ?请证明你的结论;
?请证明你的结论;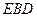 与平面
与平面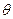 的余弦值。
的余弦值。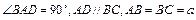 ,
,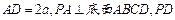 与底面成30°角.
与底面成30°角.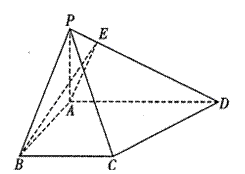
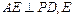 为垂足,求证:
为垂足,求证: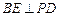 ;
;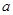 ,高为
,高为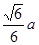 ,则此棱锥的侧面积等于( )
,则此棱锥的侧面积等于( )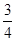
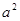
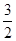
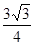

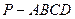 底面正方形的边长为4cm,高PO与斜高PE的夹角为
底面正方形的边长为4cm,高PO与斜高PE的夹角为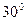 ,如图,求正四棱锥的表面积与体积
,如图,求正四棱锥的表面积与体积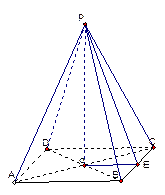
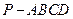 中,
中,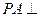 平面
平面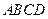 ,底面
,底面 是直角梯形,
是直角梯形,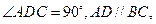
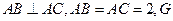 为
为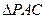
 的重心,
的重心,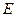 为
为 的中点,
的中点,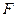 在
在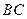 上,且
上,且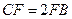 ;
;
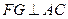 ;
;
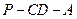 的正切值为多少时,
的正切值为多少时,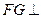 平面
平面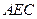 ;
;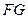 与平面
与平面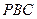 所
所 成角
成角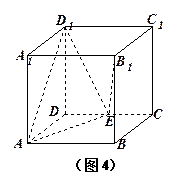
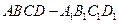 中,点E在棱CD上。
中,点E在棱CD上。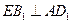 ;
;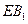 与平面
与平面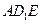 所成的角;
所成的角;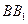 上,且
上,且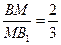 ,是否存在点E,使平面
,是否存在点E,使平面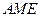 ,若存在,指出点E的位置,若不存在,请说明理由。
,若存在,指出点E的位置,若不存在,请说明理由。 的边长为4,
的边长为4, 是
是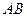 边上的高,
边上的高, 分别是
分别是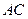 和
和 边的中点,现将△
边的中点,现将△ .
. 的位置关系,并说明理由;
的位置关系,并说明理由; 的余弦值;
的余弦值; ,使
,使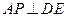 ?证明你的结论.
?证明你的结论.