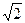题目内容
已知球O的半径为2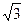
，两个平面分别截球面得到两个圆⊙O1与⊙O2，若
OO1=OO2=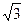，∠O1OO2=60°，则⊙O1与⊙O2的公共弦长为 。
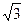，两个平面分别截球面得到两个圆⊙O1与⊙O2，若OO1=OO2=
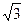，∠O1OO2=60°，则⊙O1与⊙O2的公共弦长为 。4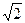
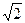
略
练习册系列答案
相关题目
题目内容
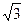，两个平面分别截球面得到两个圆⊙O1与⊙O2，若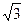，∠O1OO2=60°，则⊙O1与⊙O2的公共弦长为 。
.
大值时，求异面直线AP与SD所成角的余弦值．
中，
，
，
，
是
边的中点.
； 
∥面
． 
中，点
是矩形
的对角线的交点，三角形
是等边三角形，棱
且
．
平面
，
，
，
与平面
和矩形
所在的平面相互垂直，已知
，
.
平面
；
的大小.
关于直线
对称，
．把
沿
折起（如图二），使二面角
的余弦值等于
．对于图二，
；
平面
；
所成角的正弦值．
中，
，
，
、
分别为
、
的中点，
的延长线交
于
。现将
沿
，连接
.
：平面
平面
；
时，求二面角
中， AB=1，
，∠ABC=60
.
；
—B的余弦值。 
，
与底面成30°角.
为垂足，求证：
;