题目内容
已知函数
．
（1）讨论函数
在定义域内的极值点的个数；
（2）若函数在
处取得极值，对
,
恒成立，
求实数
的取值范围.
（1）当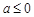
时
在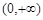
上没有极值点，当
时，在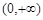上有一个极值点（2）
解析
练习册系列答案
名校通行证有效作业系列答案
相关题目
名校通行证有效作业系列答案题目内容
已知函数．
（1）讨论函数在定义域内的极值点的个数；
（2）若函数在处取得极值，对,恒成立，
求实数的取值范围.
（1）当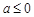时在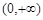上没有极值点，当时，在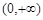上有一个极值点（2）
解析
名校通行证有效作业系列答案
.
在
上是增函数，求实数
的取值范围；
是
上的最小值和最大值.
是定义在
上的奇函数，当
时，
，使得当
的最小值是4？如果存在，求出
如果函数
的图像在函数
的图像的下方，则称函数
时，函数
上被函数
覆盖。
x3－
x2＋ax．
．
时,求函数
的图象在点
处的切线方程；
(
) 
的单调递减区间；
，
（1）若函数
在
处与直线
相切；
的值； ②求函数
上的最大值;
时，若不等式
对所有的
都成立，求实数
的取值范围.
是奇函数，且图像在点
为自然对数的底数）处的切线斜率为3.
、
的值;
，且
对任意
恒成立，求
的最大值;
时，证明：
的单调减区间；
满足，
求证：
；
，
为数列
的前
项和，求证：
。