题目内容
6.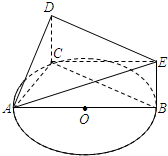 如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.(Ⅰ)求证:DE⊥平面ACD;
(Ⅱ)当三棱锥C-ADE体积最大时,求平面AED与平面ABE所成的锐二面角的余弦值.
分析 (Ⅰ)BC⊥AC,CD⊥BC.推出DE⊥平面ACD,证明DE∥BC,即可证明:DE⊥平面ACD;
(Ⅱ)当三棱锥C-ADE体积最大时,$AC=BC=2\sqrt{2}$,建立空间直角坐标系,求出平面AED与平面ABE的法向量,利用向量的夹角公式求平面AED与平面ABE所成的锐二面角的余弦值.
解答 (Ⅰ)证明:∵DC⊥面ABC,∴DC⊥BC,又∵AB是⊙O的直径,∴AC⊥BC
AC∩DC=C,AC,DC?面ACD,∴BC⊥平面ACD
又∵DC∥EB,DC=EB,∴四边形BCDE是平行四边形,∴DE∥BC
∴DE⊥平面ACD …(5分)
(Ⅱ)解:∵AC2+BC2=AB2=16${V_{C-ADE}}={V_{E-ACD}}=\frac{1}{3}{S_{△ACD}}•DE=\frac{1}{3}•\frac{1}{2}•1•AC•BC=\frac{1}{6}AC•BC≤\frac{1}{6}•\frac{{A{C^2}+B{C^2}}}{2}=\frac{4}{3}$当且仅当$AC=BC=2\sqrt{2}$时取等号,
∴当三棱锥C-ADE体积最大时,$AC=BC=2\sqrt{2}$
如图,以C为原点建立空间直角坐标系,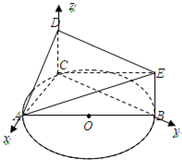
则$A({2\sqrt{2},0,0}),D({0,0,1}),B({0,2\sqrt{2},0}),E({0.2\sqrt{2},1})$$\overrightarrow{AD}=({-2\sqrt{2},0,1}),\overrightarrow{DE}=({0,2\sqrt{2},0})$,设平面ADE的一个法向量$\overrightarrow{n_1}=({x,y,z})$,则$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{AD}=-2\sqrt{2}x+z=0\\ \overrightarrow{n_1}•\overrightarrow{DE}=2\sqrt{2}y=0\end{array}\right.$,令x=1得$\overrightarrow{n_1}=({1,0,2\sqrt{2}})$
设平面ABE的一个法向量$\overrightarrow{n_2}=({x,y,z})$,$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{AB}=-2\sqrt{2}x+2\sqrt{2}y=0\\ \overrightarrow{n_1}•\overrightarrow{BE}=z=0\end{array}\right.$,
令x=1得$\overrightarrow{n_2}=({1,1,0})$,$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|{\overrightarrow{n_1}}|•|{\overrightarrow{n_2}}|}}=\frac{1}{{3•\sqrt{2}}}=\frac{{\sqrt{2}}}{6}$
∴当三棱锥C-ADE体积最大时,平面AED与平面ABE所成的锐二面角的余弦值为$\frac{{\sqrt{2}}}{6}$…(13分)
点评 本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

 智慧小复习系列答案
智慧小复习系列答案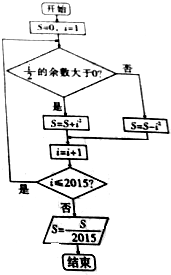
| A. | 1006 | B. | 1008 | C. | 2015 | D. | 2016 |
| A. | $\frac{{\sqrt{5}}}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{5}}}{6}$ | D. | 2 |
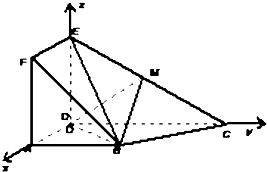 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.