题目内容
18.在△ABC中,E为AC上一点,且$\overrightarrow{AC}=4\overrightarrow{AE}$,P为BE上一点,且$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$(m>0,n>0),则$\frac{1}{m}+\frac{1}{n}$取最小值时,向量$\overrightarrow{a}$=(m,n)的模为( )| A. | $\frac{{\sqrt{5}}}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{5}}}{6}$ | D. | 2 |
分析 由题意和平面向量基本定理可得m和n的关系,由基本不等式可得式子取最小值时的m和n的值,由向量的模长公式可得.
解答 解:∵$\overrightarrow{AC}=4\overrightarrow{AE}$,∴$\overrightarrow{AP}=m\overrightarrow{AB}+n\overrightarrow{AC}$=m$\overrightarrow{AB}$+4n$\overrightarrow{AE}$,
又∵P为BE上一点,不妨设$\overrightarrow{BP}$=λ$\overrightarrow{BE}$,(0<λ<1),
∴$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=$\overrightarrow{AB}$+λ$\overrightarrow{BE}$=$\overrightarrow{AB}$+λ($\overrightarrow{AE}-\overrightarrow{AB}$)
=(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AE}$,
∴m$\overrightarrow{AB}$+4n$\overrightarrow{AE}$=(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AE}$,
∵$\overrightarrow{AB}$,$\overrightarrow{AE}$不共线,∴$\left\{\begin{array}{l}{m=1-λ}\\{4n=λ}\end{array}\right.$,∴m+4n=1,
∴$\frac{1}{m}+\frac{1}{n}$=($\frac{1}{m}+\frac{1}{n}$)(m+4n)=5+$\frac{4n}{m}$+$\frac{m}{n}$
≥5+2$\sqrt{\frac{4n}{m}•\frac{m}{n}}$=9
当且仅当$\frac{4n}{m}$=$\frac{m}{n}$即m=$\frac{1}{3}$且n=$\frac{1}{6}$时,上式取到最小值,
∴向量$\overrightarrow{a}$=(m,n)的模|$\overrightarrow{a}$|=$\sqrt{{m}^{2}+{n}^{2}}$=$\frac{\sqrt{5}}{6}$
故选:C
点评 本题考查基本不等式和平面向量基本定理以及向量的模长公式,属中档题.

| A. | 0 | B. | 1 | C. | $\frac{16}{27}$ | D. | $\frac{32}{27}$ |
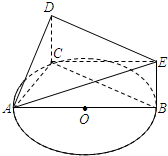 如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.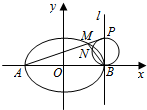 已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.
已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.