题目内容
1.设数列{an}满足(6n-3)an=(2n+1)an-1+4n2-2n+1(n≥2),a1=2,设bn=$\frac{{a}_{n}-n}{2n+1}$.(1)求证:{bn}是等比数列;
(2)设{an}的前n项和Sn,求$\frac{{S}_{n}+20}{n}$+$\frac{{n}+2}{n}$($\frac{1}{3}$)n的最小值.
分析 (1)由条件求得an,通过化简整理可得,$\frac{{a}_{n}-n}{2n+1}$=$\frac{{a}_{n-1}-(n-1)}{3(2n-1)}$,结合条件和等比数列的定义,即可得证;
(2)求得bn,an,运用分组求和和错位相减法求得{an}的前n项和Sn,化简整理,再由基本不等式,注意检验n为正整数,即可得到最小值.
解答 (1)证明:(6n-3)an=(2n+1)an-1+4n2-2n+1(n≥2),
可得an=$\frac{(2n+1){a}_{n-1}+4{n}^{2}-2n+1}{6n-3}$,
an-n=$\frac{(2n+1){a}_{n-1}-(2n+1)(n-1)}{3(2n-1)}$,
即有$\frac{{a}_{n}-n}{2n+1}$=$\frac{{a}_{n-1}-(n-1)}{3(2n-1)}$,
则bn=$\frac{1}{3}$bn-1,
故{bn}是首项为$\frac{{a}_{1}-1}{3}$=$\frac{1}{3}$,公比为$\frac{1}{3}$的等比数列;
(2)解:bn=$\frac{{a}_{n}-n}{2n+1}$=($\frac{1}{3}$)n,
则an=n+(2n+1)•($\frac{1}{3}$)n,
{an}的前n项和Sn=$\frac{n(n+1)}{2}$+Tn,
Tn=3$•\frac{1}{3}$+5•$\frac{1}{9}$+…+(2n+1)•($\frac{1}{3}$)n,
$\frac{1}{3}$Tn=3•$\frac{1}{9}$+5•$\frac{1}{27}$+…+(2n+1)•($\frac{1}{3}$)n+1,
两式相减可得$\frac{2}{3}$Tn=1+2($\frac{1}{9}$+$\frac{1}{27}$+…+$\frac{1}{{3}^{n}}$)-(2n+1)•($\frac{1}{3}$)n+1,
=1+2•$\frac{\frac{1}{9}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}$-(2n+1)•($\frac{1}{3}$)n+1,
化简可得Tn=2-$\frac{n+2}{{3}^{n}}$,
即有Sn=$\frac{n(n+1)}{2}$+2-$\frac{n+2}{{3}^{n}}$,
则$\frac{{S}_{n}+20}{n}$+$\frac{{n}+2}{n}$($\frac{1}{3}$)n=$\frac{n+1}{2}$+$\frac{2}{n}$+$\frac{20}{n}$
=$\frac{n}{2}$+$\frac{22}{n}$+$\frac{1}{2}$,
由$\frac{n}{2}$+$\frac{22}{n}$≥2$\sqrt{\frac{n}{2}•\frac{22}{n}}$=2$\sqrt{11}$,
当且仅当$\frac{n}{2}$=$\frac{22}{n}$,即n=2$\sqrt{11}$,取得等号,
由于n为正整数,当n=6时,$\frac{n}{2}$+$\frac{22}{n}$=$\frac{20}{3}$,
当n=7时,$\frac{n}{2}$+$\frac{22}{n}$=$\frac{93}{14}$<$\frac{20}{3}$,
则有n=7时,取得最小值,且为$\frac{50}{7}$.
点评 本题考查等比数列的定义和通项公式及求和公式的运用,同时考查数列的求和方法:分组求和和错位相减法,考查运算能力,属于中档题.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案| A. | 向左平移$\frac{π}{12}$ | B. | 向右平移$\frac{π}{12}$ | C. | 向左平移$\frac{π}{6}$ | D. | 向右平移$\frac{π}{6}$ |
表1
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
(2)由于以上统计数据填下面2×2列联表(填写在答题卡的2×2列联表中),并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
| A. | 0 | B. | 1 | C. | $\frac{16}{27}$ | D. | $\frac{32}{27}$ |
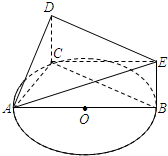 如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.