题目内容
为了了解青少年视力情况,某市从高考体检中随机抽取16名学生的视力进行调查,经医生用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下: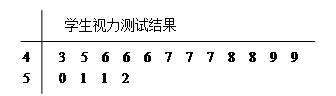
(1)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(2)以这16人的样本数据来估计该市所有参加高考学生的的总体数据,若从该市参加高考的学生中任选3人,记 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.
(1)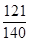 ;(2)分布列为
;(2)分布列为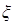

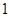
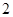
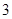
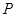
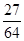
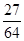
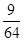
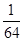
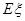
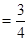 .
.
解析试题分析:(1)注意事件“至多有1人是“好视力”的”等于事件“恰有0人是“好视力”的”与“恰有有1人是“好视力”的”的和,而这两个事件是互斥事件,先算出这两个事件的概率,由互斥事件的概率和公式就可求得所求的概率;(2)首先写出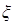 的所有可能取值为0、1、2、3,既然是以以这16人的样本数据来估计该市所有参加高考学生的的总体数据,则从该市参加高考的学生中任选1人是“好视力”学生的概率为
的所有可能取值为0、1、2、3,既然是以以这16人的样本数据来估计该市所有参加高考学生的的总体数据,则从该市参加高考的学生中任选1人是“好视力”学生的概率为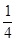 ,不是“好视力”学生的概率为
,不是“好视力”学生的概率为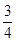 ,抽3人就是将“每次抽1人”的试验重复做三次,所以
,抽3人就是将“每次抽1人”的试验重复做三次,所以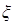 服从参数为3和
服从参数为3和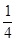 的二项分布,由n次独立重复试验恰有k次发生的概率公式
的二项分布,由n次独立重复试验恰有k次发生的概率公式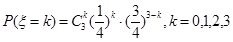 可求得
可求得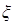 的分布列,进而可求得其数学期望.
的分布列,进而可求得其数学期望.
试题解析:(1)设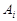 表示所取3人中有
表示所取3人中有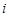 个人是“好视力”,至多有1人是“好视力”记为事件
个人是“好视力”,至多有1人是“好视力”记为事件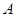 ,
,
则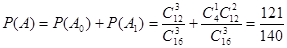 6分
6分
(2)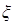 的可能取值为0、1、2、3 7分
的可能取值为0、1、2、3 7分 ;
; 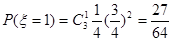
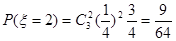 ;
;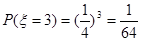
分布列为
10分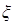

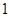
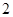
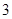
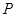
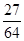
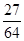
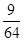
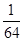
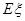
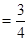 . 12分
. 12分
考点:1.古典概率;2.互斥事件的概率和公式;3.二项分布与数学期望.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目

 (元).求随机变量
(元).求随机变量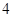 名男生和
名男生和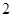 名女生中任选
名女生中任选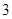 人参加演讲比赛,
人参加演讲比赛,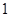 名女生的概率;
名女生的概率; .
.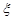 的数学期望和方差.
的数学期望和方差.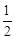 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是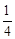 .
.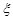 的数学期望.
的数学期望. 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为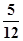 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为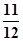 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品. 个,设
个,设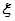 表示其中合格品的个数,求
表示其中合格品的个数,求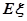 .
.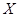 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求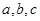 满足
满足 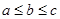 ,则称
,则称 为这三个数的中位数).
为这三个数的中位数).