题目内容
2008年5月12日,四川汶川发生8.0级特大地震,通往灾区的道路全部中断. 5月12日晚,抗震救灾指挥部决定从水路(一支队伍)、陆路(东南和西北两个方向各一支队伍)和空中(一支队伍)同时向灾区挺进.在5月13日,仍时有较强余震发生,天气状况也不利于空中航行. 已知当天从水路抵达灾区的概率是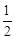 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是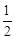 ,从空中抵达灾区的概率是
,从空中抵达灾区的概率是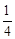 .
.
(1)求在5月13日恰有1支队伍抵达灾区的概率;
(2)求在5月13日抵达灾区的队伍数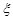 的数学期望.
的数学期望.
(1) .(2)
.(2)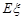 =
=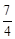 .
.
解析试题分析:(1)依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且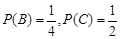 .根据独立事件概率的计算公式即得.
.根据独立事件概率的计算公式即得.
(2)设5月13日抵达灾区的队伍数为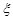 ,则
,则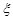 =0、1、2、3、4.
=0、1、2、3、4.
根据独立事件概率的计算公式即得分布列,进一步计算数学期望.
试题解析: (1)解法一:依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且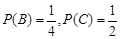 . 2分
. 2分
在5月13日恰有1支队伍抵达灾区的概率是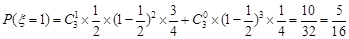 . 5分
. 5分
解法二:在5月13日恰有1支队伍抵达灾区的概率是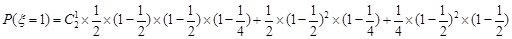
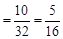 . 5分
. 5分
(2)依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且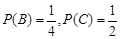 .
.
设5月13日抵达灾区的队伍数为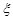 ,则
,则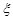 =0、1、2、3、4. 6分
=0、1、2、3、4. 6分
由已知有: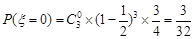 ; 7分
; 7分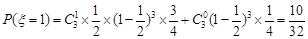 ; 8分
; 8分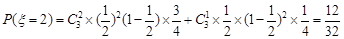 ; 9分
; 9分 ; 10分
; 10分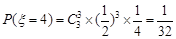 . 10分
. 10分
因此其概率分布为:
11分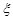
0 1 2 3 4 P 
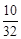
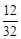
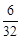
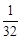
所以在5月13日抵达灾区的队伍数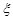 的数学期望为:
的数学期望为: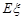 =0×
=0× + 1×
+ 1×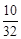 + 2×
+ 2×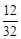 + 3×
+ 3×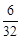

为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为
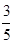 .
.(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
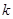 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:
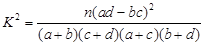 ,其中
,其中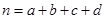 )
) 随机观测生产某种零件的某工厂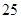 名工人的日加工零件数(单位:件),获得数据如下:
名工人的日加工零件数(单位:件),获得数据如下: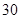 、
、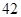 、
、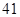 、
、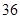 、
、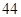 、
、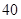 、
、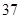 、
、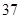 、
、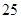 、
、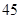 、
、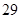 、
、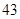 、
、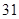 、
、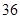 、
、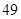 、
、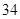 、
、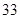 、
、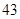 、
、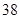 、
、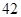 、
、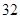 、
、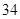 、
、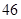 、
、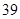 、
、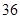 ,根据上述数据得到样本的频率分布表如下:
,根据上述数据得到样本的频率分布表如下:
| 分组 | 频数 | 频率 |
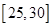 | 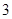 | 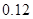 |
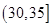 |  |  |
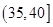 | 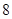 | 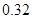 |
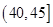 | 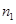 | 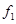 |
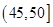 | 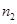 | 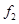 |
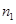 、
、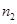 、
、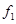 和
和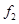 的值;
的值;(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取
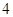 人,至少有
人,至少有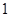 人的日加工零件数落在区间
人的日加工零件数落在区间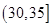 的概率.
的概率. 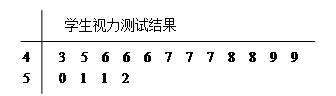
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 为取得红球的个数.
为取得红球的个数.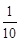 ,则n的最小值是_____________.
,则n的最小值是_____________.