题目内容
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列.
(1)0.24
(2)ξ 0 2 P 0.24 0.76
解析

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为
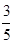 .
.(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
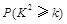 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
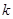 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:
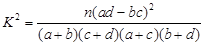 ,其中
,其中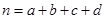 )
) 自驾游从A地到B地有甲乙两条线路,甲线路是A-C-D-B,乙线路是A-E-F-G-H-B,其中CD段,EF段,GH段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表所示.
| | CD段 | EF段 | GH段 |
| 堵车概率 | 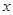 | 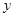 | 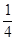 |
| 平均堵车时间 (单位:小时) |  | 2 | 1 |
经调查发现,堵车概率
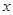 在
在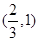 上变化,
上变化,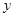 在
在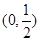 上变化.
上变化.在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计
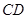 段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.| 堵车时间(单位:小时) | 频数 |
| [0,1] | 8 |
| (1, 2] | 6 |
| (2, 3] | 38 |
| (3, 4] | 24 |
| (4, 5] | 24 |
(1)求
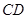 段平均堵车时间
段平均堵车时间 的值;
的值;(2)若只考虑所花汽油费的期望值大小,为了节约,求选择走甲线路的概率.
 ,停车付费多于14元的概率为
,停车付费多于14元的概率为 ,求甲停车付费6元的概率;
,求甲停车付费6元的概率;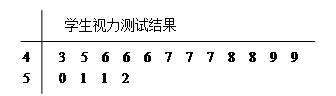
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求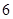 道备选题中一次性随机抽取
道备选题中一次性随机抽取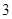 道题,按照题目要求独立完成.规定:至少正确完成其中
道题,按照题目要求独立完成.规定:至少正确完成其中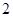 道题的便可通过.已知
道题的便可通过.已知 道题能正确完成,
道题能正确完成,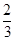 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.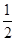 ,停车付费多于14元的概率为
,停车付费多于14元的概率为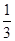 ,求甲临时停车付费恰为6元的概率;
,求甲临时停车付费恰为6元的概率;