题目内容
一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)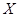 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求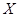 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数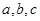 满足
满足 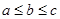 ,则称
,则称 为这三个数的中位数).
为这三个数的中位数).
(1)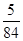 (2)详见解析.
(2)详见解析.
解析试题分析:(1)从9张卡片中任取3张,有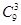 和不同的结果,其中,3张卡片上的数字完全相同的有
和不同的结果,其中,3张卡片上的数字完全相同的有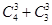 ,由于是任取的,所以每个结果出现的可能性是相等的,故可根据古典概型的概率公式求得概率;
,由于是任取的,所以每个结果出现的可能性是相等的,故可根据古典概型的概率公式求得概率;
(2)由题设随机变量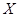 的所有可能取值有1,2,3;
的所有可能取值有1,2,3;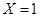 表示抽出的三第卡片上的三个数字可以是
表示抽出的三第卡片上的三个数字可以是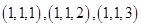
 表示抽出的三第卡片上的三个数字可以是
表示抽出的三第卡片上的三个数字可以是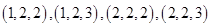
 表示抽出的三第卡片上的三个数字可以是
表示抽出的三第卡片上的三个数字可以是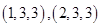
于是可用古典概型的概率公式求出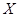 的分布列与数学期望.
的分布列与数学期望.
解:(1)由古典概型中的概率计算公式知所求概率为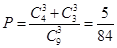
(2)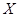 的所有可能值为1,2,3,且
的所有可能值为1,2,3,且 ,
, .
.
故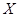 的分布列为
的分布列为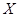
1 2 3 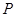
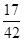
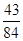
从而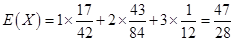
考点:1、组合;2、古典概型;3、离散型随机变量的分布列与数学期望.

练习册系列答案
相关题目
随机观测生产某种零件的某工厂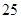 名工人的日加工零件数(单位:件),获得数据如下:
名工人的日加工零件数(单位:件),获得数据如下: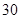 、
、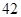 、
、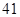 、
、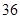 、
、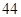 、
、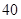 、
、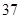 、
、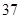 、
、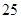 、
、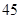 、
、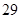 、
、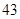 、
、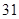 、
、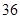 、
、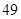 、
、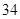 、
、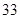 、
、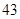 、
、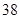 、
、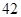 、
、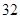 、
、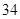 、
、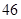 、
、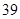 、
、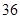 ,根据上述数据得到样本的频率分布表如下:
,根据上述数据得到样本的频率分布表如下:
| 分组 | 频数 | 频率 |
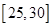 | 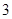 | 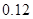 |
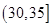 |  |  |
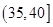 | 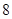 | 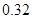 |
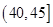 | 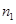 | 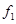 |
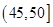 | 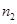 | 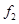 |
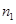 、
、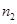 、
、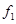 和
和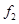 的值;
的值;(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取
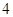 人,至少有
人,至少有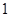 人的日加工零件数落在区间
人的日加工零件数落在区间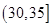 的概率.
的概率. 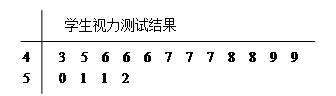
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求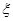 ,求
,求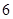 道备选题中一次性随机抽取
道备选题中一次性随机抽取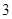 道题,按照题目要求独立完成.规定:至少正确完成其中
道题,按照题目要求独立完成.规定:至少正确完成其中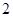 道题的便可通过.已知
道题的便可通过.已知 道题能正确完成,
道题能正确完成,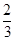 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.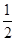 ,停车付费多于14元的概率为
,停车付费多于14元的概率为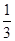 ,求甲临时停车付费恰为6元的概率;
,求甲临时停车付费恰为6元的概率;