题目内容
从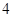 名男生和
名男生和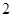 名女生中任选
名女生中任选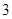 人参加演讲比赛,
人参加演讲比赛,
①求所选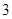 人都是男生的概率;
人都是男生的概率;
②求所选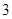 人恰有
人恰有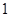 名女生的概率;
名女生的概率;
③求所选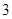 人中至少有
人中至少有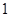 名女生的概率.
名女生的概率.
(1) ;(2)
;(2)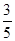 ;(3)
;(3)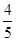 .
.
解析试题分析:本题均为组合综合应用,这类问题要注意条件的变化,例如“都”,“至少”,“恰好”,“至多”这些关键字的含义.同时也要注意数据的变化,例如,选几个人剩下几个人,有几个男生选择几个剩下几个是组合还是用排列等等.在方法的选择上要注意:是直接法还是间接法,一般简单快速准确的做出答案.
试题解析:
(1)设事件A=“所选3人均为男生”,
则P(A)= 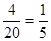 ; 4分
; 4分
(2)设事件B=“恰有1名女生”,则P(B)=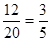 ; 8分
; 8分
(3)因为事件A表示所选3人均为男生,则事件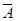 表示所选
表示所选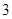 人中至少有
人中至少有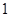 名女生,
名女生,
所以P(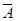 )=1-P(A)=1-
)=1-P(A)=1- =
=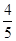 ; 12分
; 12分
考点:组合综合应用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为
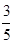 .
.(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.下面的临界值表供参考:
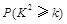 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
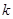 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:
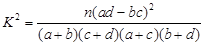 ,其中
,其中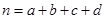 )
)  ,停车付费多于14元的概率为
,停车付费多于14元的概率为 ,求甲停车付费6元的概率;
,求甲停车付费6元的概率;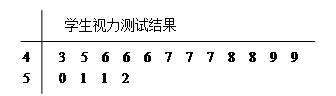
 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求