题目内容
17.从1,3,5,7,9这五个数中,每次取出两个不同的数分别为a,b,共可得到lga-lgb的不同值的个数是18.分析 因为lga-lgb=lg$\frac{a}{b}$,所以从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,共可得到lga-lgb的不同值的个数可看作共可得到多少个不同的数$\frac{b}{a}$,从1,3,5,7,9这五个数中任取2个数排列后(两数在分子和分母不同),减去相同的数字即可得到答案.
解答 解:首先从1,3,5,7,9这五个数中任取两个不同的数排列,共A52=20有种排法,
因为$\frac{3}{1}$=$\frac{9}{3}$,$\frac{1}{3}$=$\frac{3}{9}$,
所以从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,
共可得到lga-lgb的不同值的个数是:20-2=18,
故答案为:18.
点评 本题考查了排列、组合及简单的计数问题,解答的关键是想到把相等的数字去掉,属基础题.

练习册系列答案
相关题目
8.已知函数f(x)=mx2-mx+1,对一切实数x,f(x)>0恒成立,则m的范围为( )
| A. | [0,4] | B. | (0,4) | C. | (-∞,-4)∪(0,+∞) | D. | (-∞,-4)∪[0,+∞) |
5.若直线l沿x轴向左平移3各单位,再沿y轴向上平移1个单位后,回到原来的位置,则该直线l的斜率为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
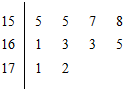 如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.
如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个数数字,从图中可以得到这10位同学身高的中位数是162.