题目内容
7．
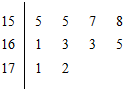如图是根据某校10位高一同学的身高（单位：cm）画出的茎叶图，其中左边的数字从左到右分别表示学生身高的百位数字和十位数字，右边的数字表示学生身高的个数数字，从图中可以得到这10位同学身高的中位数是162．
分析 根据茎叶图中的数据，结合中位数的概念，即可求出结果．
解答 解：根据茎叶图中的数据，得；
这10位同学的身高按从小到大的顺序排列，
排在第5、6的是161、163，
所以，它们的中位数是$\frac{161+163}{2}$=162．
故答案为：162．
点评 本题考查了中位数的概念与应用问题，是基础题目．
练习册系列答案
相关题目
18．下列结论正确的是（ ）
| A． | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$，则存在唯一实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B． | 已知向量$\overrightarrow{a}$，$\overrightarrow{b}$为非零向量，则“$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为钝角”的充要条件是“$\overrightarrow{a}$•$\overrightarrow{b}$＜0” | |
| C． | 若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1＞0 | |
| D． | “若θ=$\frac{π}{3}$，则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$，则cosθ$≠\frac{1}{2}$” |
2．已知C${\;}_{n}^{0}$+3C${\;}_{n}^{1}$+32C${\;}_{n}^{2}$+…+3nC${\;}_{n}^{n}$=1024，则C${\;}_{n+1}^{2}$+C${\;}_{n+1}^{3}$的值为（ ）
| A． | 21 | B． | 35 | C． | 56 | D． | 210 |
19．直线y=4x与曲线y=x3在第一象限内围成的封闭图形的面积为（ ）
| A． | 4$\sqrt{2}$ | B． | 4 | C． | 2$\sqrt{2}$ | D． | 2 |
12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线与圆x2+y2-4x+2=0，有公共点，则该双曲线离心率的取值范围是（ ）
| A． | （1，2] | B． | [$\sqrt{2}$，+∞） | C． | （1，$\sqrt{2}$] | D． | （1，$\sqrt{2}$） |