题目内容
7．正三棱锥P-ABC的侧棱两两垂直，则PA与底面ABC所成角的余弦值为$\frac{\sqrt{6}}{3}$．分析 根据所给的正三棱锥的特点，根据三垂线定理做出二面角的平面角，在直角三角形中做出要用的两条边的长度，根据三角函数的定义得到角的余弦值即可．
解答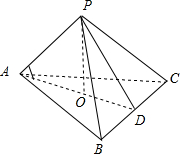 
解：正三棱锥P-ABC的侧棱两两垂直，
过P做地面的垂线PO，在面ABC上，做BC的垂线AD，
AO为PA在底面的射影，
则∠PAO就是PA与底面ABC所成角，
设侧棱长是1，在等腰直角三角形PBC中BC=$\sqrt{2}$，PD=$\frac{\sqrt{2}}{2}$，
AD=$\frac{\sqrt{6}}{2}$，
PA与底面ABC所成角的余弦值为：$\frac{PA}{AD}$=$\frac{1}{\frac{\sqrt{6}}{2}}$=$\frac{\sqrt{6}}{3}$．
故答案为：$\frac{\sqrt{6}}{3}$．
点评 本题考查二面角的平面角及其求法，本题解题的关键是做出直线与平面所成角，解三角形，是基本知识的考查．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
17．已知a=2${\;}^{-\frac{1}{3}}$，b=log2$\frac{1}{3}$，c=3${\;}^{-\frac{1}{2}}$，则a，b，c的大小关系是（ ）
| A． | c＞a＞b | B． | a＞b＞c | C． | a＞c＞b | D． | b＞c＞a |
2．已知$\overrightarrow{m}$≠$\overrightarrow{0}$，λ∈R，$\overrightarrow{a}$=$\overrightarrow{m}$+λ$\overrightarrow{n}$，$\overrightarrow{b}$=3$\overrightarrow{m}$，若$\overrightarrow{a}$∥$\overrightarrow{b}$，则（ ）
| A． | λ=0 | B． | $\overrightarrow{n}$=$\overrightarrow{0}$ | C． | $\overrightarrow{m}$∥$\overrightarrow{n}$ | D． | $\overrightarrow{m}$∥$\overrightarrow{n}$或λ=0 |