题目内容
9.设函数f(x)=sin(2x-$\frac{π}{2}$)(x∈R),则f(x)是( )| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
分析 利用三角函数的诱导公式将函数进行化简,结合三角函数的奇偶性进行判断即可.
解答 解:f(x)=sin(2x-$\frac{π}{2}$)=-sin($\frac{π}{2}$-2x)=-cos2x,
则f(x)是偶函数,
故选:B
点评 本题主要考查三角函数奇偶性的判断,根据三角函数的诱导公式进行化简是解决本题的关键.

练习册系列答案
相关题目
17.执行如图所示的程序框图,如果输入的x∈R,则输出的h(x)的最小值是( )


| A. | $\frac{3}{4}$ | B. | 3 | C. | 4 | D. | 7 |
18.已知变量x与y线性相关,数据如表:则y与x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 2 | 6 | 7 |
| A. | (1,3) | B. | (2,6) | C. | (3,7) | D. | (1.5,4) |
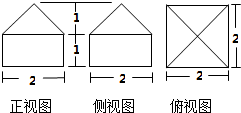 已知一几何体的三视图如图所示.
已知一几何体的三视图如图所示.