题目内容
1.设函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(15-x),x≤0}\\{f(x-2),x>0}\end{array}\right.$ 则f(3)=4,f(f(2015))=log215.分析 根据已知中函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(15-x),x≤0}\\{f(x-2),x>0}\end{array}\right.$,将自变量的值代入,分析变量的变化规律,可得答案.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(15-x),x≤0}\\{f(x-2),x>0}\end{array}\right.$,
∴f(3)=f(1)=f(-1)=log216=4,
f(f(2015))=f(f(2013))=f(f(2011))=…=f(f(1))=f(f(-1))=f(4)=f(2)=f(0)=log215,
故答案为:4,log215
点评 本题考查的知识点是分段函数的应用,函数求值,难度不大,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
9.设函数f(x)=sin(2x-$\frac{π}{2}$)(x∈R),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
11.一个算法的程序框图如图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )


| A. | i<4 | B. | i<5 | C. | i≥5 | D. | i<6 |
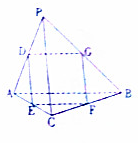 如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.
如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.