题目内容
17.在数列{an}中,a1=1,a2=6,点(an-an-1,an+1)在函数f(x)=4x的图象上(1)求证:数列{an+1-2an}是等比数列,并求出数列{an}的通项公式;
(2)数列{an}的前n项和为Sn,求证:Sn<(n-1)•2n+1+2;
(3)若Cn=3n-λ•(-1)n•$\frac{a_n}{{n-\frac{1}{2}}}$,(n∈N*,λ为非零实数),对任意n∈N*,Cn+1>Cn恒成立,求实数λ的取值范围.
分析 (1)由题意得an+1=4(an-an-1),从而可得an+1-2an=2(an-2an-1),从而判断数列{an+1-2an}是以4为首项,2为公比的等比数列;则an+1-2an=4•2n-1=2n+1,化简$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=1,从而可得an=(2n-1)2n-1;
(2)化简Sn=1+3×2+5×22+…+(2n-1)2n-1,从而可得Sn=(2n-3)2n+3,从而证明即可;
(3)化简可得2•3n+3λ(-1)n•2n>0,分当n为偶数时与当n为奇数时讨论实数λ的取值范围即可.
解答 解:(1)∵点(an-an-1,an+1)在函数f(x)=4x的图象上,
∴an+1=4(an-an-1),
∴an+1-2an=2(an-2an-1),
又∵a2-2a1=6-2=4,
∴$\frac{{a}_{n+1}-2{a}_{n}}{{a}_{n}-2{a}_{n-1}}$=2,
∴数列{an+1-2an}是以4为首项,2为公比的等比数列;
故an+1-2an=4•2n-1=2n+1;
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=1;
故{$\frac{{a}_{n}}{{2}^{n}}$}是以$\frac{1}{2}$为首项,1为公差的等差数列;
∴an=(2n-1)2n-1;
(2)证明:Sn=1+3×2+5×22+…+(2n-1)2n-1①,
2Sn=1×2+3×22+5×23+…+(2n-1)2n②,
①-②得,
-Sn=1+2(2+22+23+…+2n-1)-(2n-1)2n
=(3-2n)2n-3,
故Sn=(2n-3)2n+3,
Sn=(2n-3)2n+3=(2n-2)2n-2n+3
=(n-1)2n+1+2+(1-2n)
<(n-1)2n+1+2.
(3)Cn=3n-λ•(-1)n•$\frac{a_n}{{n-\frac{1}{2}}}$=3n-λ•(-1)n•2n;
∵对任意n∈N*,Cn+1>Cn恒成立,
∴3n+1-λ•(-1)n+1•2n+1>3n-λ•(-1)n•2n,
∴2•3n+3λ(-1)n•2n>0,
当n为偶数时,2•3n+3λ•2n>0,∴λ>-$(\frac{3}{2})^{n-1}$,故λ>-$\frac{3}{2}$;
当n为奇数时,2•3n-3λ•2n>0,∴λ<$(\frac{3}{2})^{n-1}$,故λ<1;
∴实数λ的取值范围为(-$\frac{3}{2}$,0)∪(0,1).
点评 本题考查了等差数列与等比数列的应用及数列前n项和的求法及不等式的证明,属于难题.

| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费支出为10百万元时,销售额多大?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{∑({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$.
| A. | -$\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
| A. | (1,2) | B. | [1,2] | C. | [1,2) | D. | (1,2] |
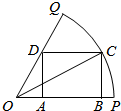 如图,已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
如图,已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.