题目内容
12.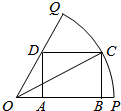 如图,已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
如图,已知OPQ是半径为$\sqrt{7}$圆心角为$\frac{π}{3}$的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.(Ⅰ)若Rt△CBO的周长为$\frac{{\sqrt{7}(2\sqrt{10}+5)}}{5}$,求$\frac{3-cos2α}{co{s}^{2}α-sinαcosα}$的值.
(Ⅱ)求$\overrightarrow{OA}•\overrightarrow{AB}$的最大值,并求此时α的值.
分析 (Ⅰ)由条件利用直角三角形中的边角关系求出三角形的周长,利用三角函数的倍角公式进行化简进行求解.
(Ⅱ)结合向量的数量积公式,结合三角函数的带动下进行求解.
解答 解:(Ⅰ)BC=OCsinα=$\sqrt{7}$sinα,OB=OCcosα=$\sqrt{7}$cosα,
则若Rt△CBO的周长为$\frac{{\sqrt{7}(2\sqrt{10}+5)}}{5}$,
则$\sqrt{7}$+$\sqrt{7}$sinα+$\sqrt{7}$cosα=$\frac{{\sqrt{7}(2\sqrt{10}+5)}}{5}$,
sinα+cosα=$\frac{2\sqrt{10}}{5}$,
平方得2sinαcosα=$\frac{3}{5}$,
即$\frac{2sinαcosα}{sin^2α+cos^2α}$=$\frac{2tanα}{1+tan^2α}$=$\frac{3}{5}$,
解得tanα=3(舍)或tanα=$\frac{1}{3}$.
则$\frac{3-cos2α}{co{s}^{2}α-sinαcosα}$=$\frac{2(cos^2α+2sin^2α)}{cos^2α-sinαcosα}$=$\frac{2(1+2tan^2α)}{1-tanα}$=$\frac{2(1+2×\frac{1}{9})}{1-\frac{1}{3}}$=$\frac{11}{3}$.
(Ⅱ)在Rt△OBC中,BC=OCsinα=$\sqrt{7}$sinα,OB=OCcosα=$\sqrt{7}$cosα,
在Rt△ODA中,
OA=DAtan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$BC=$\frac{\sqrt{21}}{3}$sinα,
∴AB=OB-OA=$\sqrt{7}$(cosα-$\frac{\sqrt{3}}{3}$cosα),
则$\overrightarrow{OA}•\overrightarrow{AB}$=|$\overrightarrow{OA}$|$\overrightarrow{AB}$|=$\sqrt{7}$(cosα-$\frac{\sqrt{3}}{3}$cosα)•$\frac{\sqrt{21}}{3}$sinα$\begin{array}{l}=\frac{{7\sqrt{3}}}{3}({cosα-\frac{{\sqrt{3}}}{3}sinα})•sinα\end{array}$$\begin{array}{l}=\frac{{7\sqrt{3}}}{3}({sinαcosα-\frac{{\sqrt{3}}}{3}{{sin}^2}α})\end{array}$$\begin{array}{l}=\frac{{7\sqrt{3}}}{3}[{\frac{1}{2}sin2α-\frac{{\sqrt{3}}}{6}({1-cos2α})}]\end{array}$$\begin{array}{l}=\frac{{7\sqrt{3}}}{3}({\frac{1}{2}sin2α+\frac{{\sqrt{3}}}{6}cos2α-\frac{{\sqrt{3}}}{6}})\end{array}$
=$\frac{{7\sqrt{3}}}{3}[{\frac{1}{{\sqrt{3}}}({\frac{{\sqrt{3}}}{2}sin2α+\frac{1}{2}cos2α})-\frac{{\sqrt{3}}}{6}}]=\frac{7}{3}sin({2α+\frac{π}{6}})-\frac{7}{6}({0<α<\frac{π}{3}})$
∵$0<α<\frac{π}{3}$,
∴$\frac{π}{6}<2α+\frac{π}{6}<\frac{5π}{6}$,
∴当$2α+\frac{π}{6}=\frac{π}{2}$,
即$α=\frac{π}{6}$时,$\overrightarrow{OA}•\overrightarrow{AB}$有最大值$\frac{7}{6}$.
点评 本题主要考查两个向量的数量积的定义,三角恒等变换,正弦函数的定义域和值域,考察学生的运算和推理能力.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |