题目内容
7.在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知A,B的极坐标分别为$(2,\frac{π}{2})$,$(\sqrt{2},\frac{π}{4})$.(1)求直线AB的直角坐标方程;
(2)圆C的参数方程为$\left\{\begin{array}{l}{x=1+2cosθ}\\{y=2sinθ}\end{array}\right.$,(θ为参数),试判断直线AB与圆C的位置关系.
分析 (1)由A,B的极坐标化为直角坐标,根据斜率公式和点斜式方程求出直线AB的方程,再化为一般式方程;
(2)将圆C的参数方程化为直角坐标系下的方程,并求出圆心坐标和半径,利用点到直线的距离公式求出圆心到直线AB的距离,再与半径比较即可得到答案.
解答 解:(1)由题意得,A,B的极坐标分别为$(2,\frac{π}{2})$,$(\sqrt{2},\frac{π}{4})$,
∴A(0,2),B(1,1),
则lAB方程为:$y=\frac{1-2}{1-0}x+2$,则y=-x+2,即x+y-2=0;
(2)∵圆C的参数方程为$\left\{\begin{array}{l}{x=1+2cosθ}\\{y=2sinθ}\end{array}\right.$,
∴圆C的标准方程为:(x-1)2+y2=4,圆心为C(1,0),半径r=2,
则圆心为C(1,0)到直线AB:x+y-2=0的距离$d=\frac{|1-2|}{\sqrt{2}}=\frac{\sqrt{2}}{2}<2$=r,
所以直线AB与圆C相交.
点评 本题考查极坐标与直角坐标、参数方程与普通方程之间的转化,点到直线之间的距离公式的应用,以及直线与圆的位置关系的判断,属于中档题.

练习册系列答案
相关题目
18.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为:$\stackrel{∧}{y}$=0.85x-85.71,则下列结论中不正确的是( )
| A. | 3与3x2+2ax+b=0具有正的线性相关关系 | |
| B. | 回归直线过样本点的中心($\overline{x}$,$\overline{y}$) | |
| C. | 若该大学某女生身高为170cm,则可断定其体重必为58.79kg | |
| D. | 若该大学某女生身高增加1cm,则其体重约增加0.85kg |
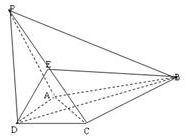 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.