题目内容
【题目】已知二次函数f(x)=x2+2bx+c(b,c∈R).
(1)若函数y=f(x)的零点为﹣1和1,求实数b,c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(﹣3,﹣2),(0,1)内,求实数b的取值范围.
【答案】
(1)解:∵﹣1,1是函数y=f(x)的零点,∴ ![]() ,解得b=0,c=﹣1
,解得b=0,c=﹣1
(2)解:∵f(1)=1+2b+c=0,所以c=﹣1﹣2b.
令g(x)=f(x)+x+b=x2+(2b+1)x+b+c=x2+(2b+1)x﹣b﹣1,
∵关于x的方程f(x)+x+b=0的两个实数根分别在区间(﹣3,﹣2),(0,1)内,
∴ 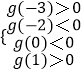 ,即
,即 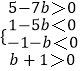 .解得
.解得 ![]() <b<
<b< ![]() ,
,
即实数b的取值范围为( ![]() ,
, ![]() )
)
【解析】(1)根据根与系数的关系列方程组解出;(2)根据f(1)=0得出b,c的关系,令g(x)=f(x)+x+b,根据零点的存在性定理列方程组解出.

练习册系列答案
相关题目
