题目内容
【题目】已知非空集合A={x|2a+1≤x≤3a﹣5}，B={x|3≤x≤22}，
（1）当a=10时，求A∩B，A∪B；
（2）求能使AB成立的a的取值范围．
【答案】
（1）解：当a=10时，A={21≤x≤25}，B={x|3≤x≤22}，
∴A∩B={x|21≤x≤22}，
A∪B={x|3≤x≤25}．
（2）解：∵A={x|2a+1≤x≤3a﹣5}，B={x|3≤x≤22}，且AB，
∴ 
，
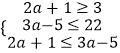解得6≤a≤9．
∴a的取值范围是[6，9]
【解析】（1）当a=10时，A={21≤x≤25}，B={x|3≤x≤22}，由此能求出A∩B和A∪B．（2）由A={x|2a+1≤x≤3a﹣5}，B={x|3≤x≤22}，且AB，知 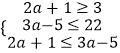，由此能求出a的取值范围．
练习册系列答案
相关题目
