Question

【题目】（本题满分15分）如图，在四棱锥中，平面PAD⊥平面ABCD， ，，E是BD的中点．

（Ⅰ）求证：EC//平面APD；

（Ⅱ）求BP与平面ABCD所成角的正切值；

（Ⅲ）求二面角的正弦值．

Answer 1

【答案】（Ⅰ）详见解析（Ⅱ）（Ⅲ）

【解析】

试题分析：（Ⅰ）证明线面平行常用到的思路就是证明平面外的直线平行于平面内的直线（Ⅱ）求BP与平面ABCD所成角首先找到斜线在平面中的射影，找到所求角，通过求解三角形三边得到角的大小（Ⅲ）利用三垂线定理作出二面角的平面角∠PGH，解三边即可求得角的正弦值

试题解析：（Ⅰ）如图，取PA中点F，连结EF、FD，

∵E是BP的中点，∴EF//AB且，

又∵∴EFDC∴四边形EFDC是平行四边形，故得EC//FD 2分

又∵EC平面PAD，FD平面PAD∴EC//平面ADE 4分

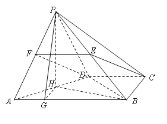
（Ⅱ）取AD中点H，连结PH，因为PA＝PD，

所以PH⊥AD

∵平面PAD⊥平面ABCD于AD ∴PH⊥面ABCD

∴HB是PB在平面ABCD内的射影 ∴∠PBH是PB与平面ABCD所成角 6分

∵四边形ABCD中，

∴四边形ABCD是直角梯形，

设AB=2a，则，在中，易得，

，又∵，

∴是等腰直角三角形，

∴

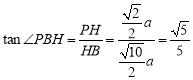∴在中， 10分

（Ⅲ）在平面ABCD内过点H作AB的垂线交AB于G点，连结PG，则HG是PG在平面ABCD上的射影，故PG⊥AB，所以∠PGH是二面角P-AB-D的平面角，由AB=2a 11分

，又∴，

在中，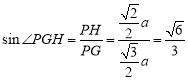

∴二面角P-AB-D的的正弦值为 15分