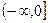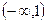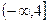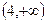题目内容
给出下列四个命题:
①若a>b>0,c>d>0,那么
<
;②已知a、b、m都是正数,并且a<b,则
>
;③若a、b∈R,则a2+b2+5≥2(2a-b);④函数f(x)=2-3x-
的最大值是2-4
.其中正确命题的序号是______把你认为正确命题的序号都填上)
①若a>b>0,c>d>0,那么
|
|
| a+m |
| b+m |
| a |
| b |
| 4 |
| x |
| 3 |
a>b>0,c>d>0,
∴0<
<
且0<b<a
所以0<
<
⇒
<
,故①不正确;
对于②,
-
=
∵b>0,m>0,b+m>0,b-a>0
∴
-
>0,故
>
,②正确;
对于③,∵(a2+b2+5)-2(2a-b)=(a-2)2+(b-1)2≥0,
∴对任意a、b∈R,都有a2+b2+5≥2(2a-b),故③正确;
对于④,∵f(x)=2-3x-
=2-(3x+
),
且|3x+
|≥2
=4
,得3x+
≤-4
或3x+
≥4
,
∴f(x)=2-3x-
的值域为(-∞,2-4
]∪[2+4
,+∞),
所以函数没有最大值,故④不正确.
故答案为:②③
∴0<
| 1 |
| c |
| 1 |
| d |
所以0<
| b |
| c |
| d |
| a |
|
|
对于②,
| a+m |
| b+m |
| a |
| b |
| m(b-a) |
| b(b+m) |
∵b>0,m>0,b+m>0,b-a>0
∴
| a+m |
| b+m |
| a |
| b |
| a+m |
| b+m |
| a |
| b |
对于③,∵(a2+b2+5)-2(2a-b)=(a-2)2+(b-1)2≥0,
∴对任意a、b∈R,都有a2+b2+5≥2(2a-b),故③正确;
对于④,∵f(x)=2-3x-
| 4 |
| x |
| 4 |
| x |
且|3x+
| 4 |
| x |
| 3×4 |
| 3 |
| 4 |
| x |
| 3 |
| 4 |
| x |
| 3 |
∴f(x)=2-3x-
| 4 |
| x |
| 3 |
| 3 |
所以函数没有最大值,故④不正确.
故答案为:②③

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
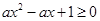 恒成立,则实数a的取值范围为 ________;
恒成立,则实数a的取值范围为 ________; 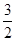 ,+∞),f(
,+∞),f(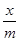 )-4m2f(x)≤f(x-1)+4f(m)恒成立,则实数m的取值范围是________.
)-4m2f(x)≤f(x-1)+4f(m)恒成立,则实数m的取值范围是________.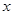 的不等式
的不等式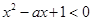 的解集是空集”是假命题,则实数
的解集是空集”是假命题,则实数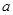 的取值范围是_______.
的取值范围是_______.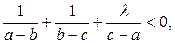 对满足
对满足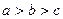 恒成立,则
恒成立,则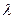 的取值范围是( )
的取值范围是( )