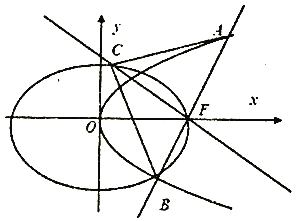
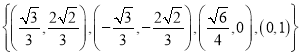题目内容
【题目】已知椭圆
的短轴长为
，且椭圆的一个焦点在圆
上.
（1）求椭圆的方程；
（2）已知椭圆的焦距小于
，过椭圆的左焦点
的直线
与椭圆相交于
两点，若
，求
【答案】（1）
或
.（2）
【解析】
（1）由题意可知：b＝1，由焦点在圆上，可求得c，进而求得a，即可求得椭圆方程；
（2设出直线l的方程，代入椭圆，得到A、B的纵坐标的关系，利用向量转化的纵坐标的关系，求得直线方程，利用弦长公式可得所求．
（1）因为椭圆的短轴长为
，所以
，则
.
圆
与
轴的交点为
，
，
故
或
，
从而
或
，
故椭圆的方程为或.
（2）设
，
，由
，得
.
因为椭圆的焦距小于
，所以椭圆的方程为，
当直线
的斜率为0时，AF=
,BF=
,不满足题意，
所以将的方程设为
，代入椭圆方程，消去，得
，
所以
，
，
将代入，得
.
故
.
练习册系列答案
轻松暑假总复习系列答案
相关题目
